| Issue |
J. Eur. Opt. Society-Rapid Publ.
Volume 21, Number 2, 2025
|
|
|---|---|---|
| Article Number | 35 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/jeos/2025032 | |
| Published online | 31 July 2025 | |
Research Article
Generation of nondiffracting radial carpet-lattice beams by using an extended Durnin’s setup
1
College of Modern Science and Technology, China Jiliang University, Jinhua, Zhejiang, 321004, PR China
2
Key Laboratory of Optical Information Detecting and Display Technology, Zhejiang Normal University, Jinhua, Zhejiang, 321004, PR China
* Corresponding author: renzhijun@zjnu.cn
Received:
16
April
2025
Accepted:
3
July
2025
In the past, the researchers have generated radial carpet beams, a type of 2D optical lattice with polar symmetry. However, the classical radial carpet beams expand slowly as they propagate, that is, they are not nondiffracting beams. By introducing an extended Durnin’s experimental setup equipped with an amplitude-type spatial light modulator loaded with the angular spectrum of a radial grating function, which is distributed along narrow annular pupils, we generated and demonstrated a type of nondiffracting radial carpet-lattice beam. Different from classical radial carpet beams that slowly expand during propagation, the generated nondiffracting radial carpet-lattice beams are propagation-invariant, hence termed nondiffracting radial carpet-lattice beams.
Key words: Radial carpet-lattice beams / Radial gratings / Durnin’s experimental setup / Amplitude-type spatial light modulator
© The Author(s), published by EDP Sciences, 2025
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In 2018, Rasouli and his research team introduced an important class of lattice beams, named combined half-integer Bessel-like beams [1]. These lattice beams are generated based on the near-field diffraction of radial gratings. By utilizing different radial gratings, several types of combined half-integer Bessel beams – including radial carpet beams, petal-like beams, and annular vortex beams are generated successively. Among them, radial carpet beams [2–4] exhibit unprecedented 2D optical lattices with polar symmetry. Here, we term the carpet beams featuring a radial lattices optical structure as carpet-lattice beams. Nondiffracting or propagation-invariant optical fields do not present spreading or change in their transverse intensity distribution as they propagate within a finite distance determined by the optical setup. However, classical radial carpet beams expand slowly during propagation. Hence, although their optical structure is maintained, they are not strictly propagation-invariant and thus do not qualify as nondiffracting beams.
The defining characteristic of a nondiffracting beam is the presence of a single longitudinal wavenumber. This implies that nondiffracting beams possess a cone-like angular spectrum that can be mathematically described by the Dirac delta function δ(v–v 0). In 1987, Durnin proposed and generated the first practical nondiffracting beams: zero-order Bessel beam [5]. Bessel beams are exact solutions to the scalar Helmholtz equation in cylindrical coordinates, with their amplitude governed by the Bessel function of the first kind. To generate these beams, Durnin and coworkers placed an annular slit in the front focal plane of a lens. This configuration modulated the incident diffracting wavefront, converting it into a conical wave. Subsequently, researchers generate other nondiffracting beams, such as high-order Bessel beams [6, 7], Mathieu beams [8–10] and parabolic beams [11, 12], using Durnin’s setup.
In our scheme, we extend Durnin’s original setup by creating an annular pupil aperture in the Fourier plane. This aperture incorporates arbitrary azimuthal amplitude components to generate nondiffracting radial carpet-lattice beams. An amplitude-type spatial light modulator (SLM) serves as the key component for angular pupil modulation. In modern optics, SLMs are important modulation element widely used to dynamically generate nondiffracting beams with complex profiles [13–15]. Building upon this principle, an extended version of Durnin’s experimental setup can be constructed. By loading the spectral information of radial gratings onto the annular slit, we generate a family of nondiffracting radial carpet-lattice beams in the plane after the Fourier transform lens.
2 Theory
All nondiffracting beams must satisfy the condition that their transverse spatial frequency components are the same [16], that is, the general Fourier spectrum of a nondiffracting beam is located on a circular ring in the corresponding Fourier plane. In our scheme, the annular slit modulated by the radial grating with complex amplitude information is placed at the focal plane in front of the lens. Hence, the Fourier spectrum of a nondiffracting beam can conveniently be written in polar coordinates as: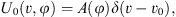 (1)where ν is a radial spatial frequency, and δ is the Dirac delta function that can limit the spectral distribution to a circular ring with radius ν
0. A(φ) gives the complex Fourier spectrum on this circular ring as a function of the azimuthal angle φ. In the extended Durnin’s experimental setup, the Fourier spectrum U
0(v, φ) can be regarded as the transmission function of modulating element. In our work, A(φ) is a complex amplitude function of the radial grating that resides on an annular slit of radius v
0, and its Fourier expansion function can be written as:
(1)where ν is a radial spatial frequency, and δ is the Dirac delta function that can limit the spectral distribution to a circular ring with radius ν
0. A(φ) gives the complex Fourier spectrum on this circular ring as a function of the azimuthal angle φ. In the extended Durnin’s experimental setup, the Fourier spectrum U
0(v, φ) can be regarded as the transmission function of modulating element. In our work, A(φ) is a complex amplitude function of the radial grating that resides on an annular slit of radius v
0, and its Fourier expansion function can be written as: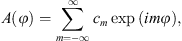 (2)where c
m
is mth Fourier series coefficient, m is the number of spokes of the grating. On the basis of the diffraction integral in cylindrical coordinates, the light field distribution in the front surface of the Fourier transforming lens can be written as:
(2)where c
m
is mth Fourier series coefficient, m is the number of spokes of the grating. On the basis of the diffraction integral in cylindrical coordinates, the light field distribution in the front surface of the Fourier transforming lens can be written as:![$$ \begin{array}{c}{U}_1\left({\rho }^{\prime},{\theta }^{\prime}\right)=\frac{1}{{i\lambda f}}{\iint }_{-\infty }^{\infty }{U}_0\left(v,\phi \right)\mathrm{exp}\left[\frac{{ik}}{2f}\left({v}^2+{\rho }^{\prime2}\right)\right]\\ \times \mathrm{exp}\left[-\frac{{ik}}{f}{\rho }^{\prime}v\mathrm{cos}(\phi -{\theta }^{\prime})\right]v\mathrm{d}v\mathrm{d}\phi,\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq3.gif) (3)where k = 2π/λ is the wave number, and λ is the wavelength of the light beam. U(ρ′, θ′) represents the complex amplitude distribution of the light field in the front surface of Fourier lens, ρ′ and θ′ are the radial distance and azimuth angle of the beam in the front surface of Fourier lens, respectively, and f is the focal length.
(3)where k = 2π/λ is the wave number, and λ is the wavelength of the light beam. U(ρ′, θ′) represents the complex amplitude distribution of the light field in the front surface of Fourier lens, ρ′ and θ′ are the radial distance and azimuth angle of the beam in the front surface of Fourier lens, respectively, and f is the focal length.
In accordance with the following Jacobi-Anger expression [17]: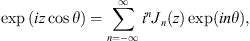 (4)where J
n
is the nth first type of Bessel function. One can obtain:
(4)where J
n
is the nth first type of Bessel function. One can obtain:![$$ \mathrm{exp}\left[-\frac{{ik}}{f}{\rho v}{cos}\left(\phi -\theta \right)\right]=\sum_{n=-\infty }^{\infty }{(-i)}^n{J}_n\left(\frac{k}{f}{\rho v}\right)\mathrm{exp}\left[-{in}\left(\phi -\theta \right)\right].\enspace $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq5.gif) (5)
(5)
Equations (1), (2) and (5) are substituted into equation (3), one can obtain:![$$ \begin{array}{c}{U}_1\left({\rho }^{\prime},{\theta }^{\prime}\right)=\frac{1}{{i\lambda f}}\mathrm{exp}\left(\frac{{ik}}{2f}{\rho }^{\prime2}\right)\\ \times {\int }_0^{\infty }\delta \left(v-{v}_0\right)\mathrm{exp}\left(\frac{{ik}}{2f}{v}^2\right){J}_n\left(\frac{k}{f}{\rho }^{\prime}v\right)v\mathrm{d}v,\\ \times {\int }_0^{2\pi }\sum_{m=-\infty }^{\infty }{c}_m\mathrm{exp}\left({im\phi }\right)\sum_{n=-\infty }^{\infty }{(-i)}^n\mathrm{exp}\left[-{in}\left(\phi -{\theta }^{\prime}\right)\right]\mathrm{d}\phi.\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq6.gif) (6)
(6)
The integrals of ![$ {\int }_0^{2\pi }\mathrm{exp}\left[i\left(m-n\right)\phi \right]\mathrm{d}\phi =2\pi {\delta }_{m,n}\enspace $](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq7.gif) and Dirac delta function δ is used, when m = n, we can get:
and Dirac delta function δ is used, when m = n, we can get:![$$ {\int }_0^{2\pi }\sum_{m=-\infty }^{\infty }{c}_m\mathrm{exp}\left({im\phi }\right)\sum_{n=-\infty }^{\infty }{(-i)}^n\mathrm{exp}\left[-{in}\left(\phi -{\theta }^{\prime}\right)\right]\enspace \mathrm{d}\phi =2\pi \sum_{m=-\infty }^{\infty }{\left(-1\right)}^m{c}_m\mathrm{exp}\left({im}{\theta }^{\prime}\right) $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq8.gif) (7)
(7)
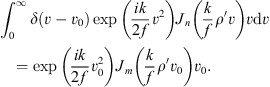 (8)
(8)
Thus the light field distribution in the front surface of the Fourier transform lens can be obtained: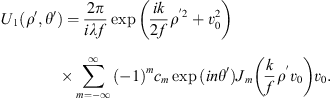 (9)
(9)
Ignoring the constants that do not affect the light intensity distribution, the field distribution through the lens is: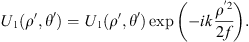 (10)
(10)
In the plane of (ρ, θ, z) after the lens, the Fresnel diffraction integral of the light field distribution is:![$$ \begin{array}{c}U\left(\rho,\theta,z\right)=\frac{1}{{i\lambda f}}\mathrm{exp}({ikz}){\iint }_{-\infty }^{\infty }{U}_1^{\prime}\left({\rho }^{\prime},{\theta }^{\prime}\right)\mathrm{exp}\left[\frac{{ik}}{2z}\left({\rho }^2+{\rho }^{\prime2}\right)\right]\\ \times \mathrm{exp}\left[-\frac{{ik}}{f}{\rho }^{\prime}\rho \mathrm{cos}({\theta }^{\prime}-\theta )\right]{\rho }^{\prime}d{\rho }^{\prime}{d\theta }.\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq12.gif) (11)
(11)
Substituting 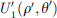 into equation (11) yields, there is:
into equation (11) yields, there is:![$$ \begin{array}{c}U\left(\rho,\theta,z\right)=\frac{2\pi }{{\lambda }^2{zf}}\mathrm{exp}({ikz})\mathrm{exp}\left(\frac{{ik}}{2f}{v}_0^2\right)\mathrm{exp}\left(\frac{{ik}}{2f}{\rho }^2\right)\\ \times \sum_{m=-\infty }^{\infty }{\left(-i\right)}^m{c}_m{v}_0{\int }_0^{\infty }{J}_m\left(\frac{k}{f}{\rho }^\mathrm{\prime}{v}_0\right)\mathrm{exp}\left(\frac{{ik}}{2z}{\rho }^{\prime2}\right){\rho }^{\prime}\mathrm{d}{\rho }^{\prime}\\ \times {\int }_0^{2\pi }\mathrm{exp}\left({im}{\theta }^{\prime}\right)\mathrm{exp}\left[-\frac{{ik}}{f}{\rho }^{\prime}\rho \mathrm{cos}({\theta }^{\prime}-\theta )\right]d{\theta }^{\prime}.\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq14.gif) (12)
(12)
Using equation (5) and the integrals of ![$ {\int }_0^{2\pi }\mathrm{exp}[i(m-n)\phi ]\mathrm{d}\phi =2\pi {\delta }_{m,n}$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq15.gif) , the following expression can be obtained:
, the following expression can be obtained: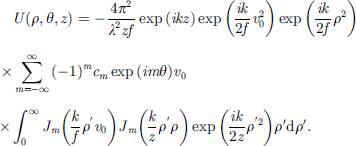 (13)
(13)
In accordance with Euler’s formula, equation (13) can be written as:![$$ \begin{array}{c}U\left(\rho,\theta,z\right)=-\frac{4{\pi }^2}{{\lambda }^2{zf}}\mathrm{exp}\left({ikz}\right)\mathrm{exp}\left(\frac{{ik}}{2f}{v}_0^2\right)\mathrm{exp}\left(\frac{{ik}}{2f}{\rho }^2\right)\\ \times \sum_{m=-\infty }^{\infty }{\left(-1\right)}^m{c}_m\mathrm{exp}\left({im\theta }\right){v}_0\\ \times \left[\begin{array}{c}{\int }_0^{\infty }{J}_m\left(\frac{k}{f}{\rho }^\mathrm{\prime}{v}_0\right){J}_m\left(\frac{k}{z}{\rho }^\mathrm{\prime}\rho \right)\mathrm{exp}\left(\frac{k}{2z}{\rho }^{\prime2}\right){\rho }^{\prime}\mathrm{d}{\rho }^{\prime}\\ +i{\int }_0^{\infty }{J}_m\left(\frac{k}{f}{\rho }^\mathrm{\prime}{v}_0\right){J}_m\left(\frac{k}{z}{\rho }^\mathrm{\prime}\rho \right)\mathrm{exp}\left(\frac{k}{2z}{\rho }^{\prime2}\right){\rho }^{\prime}\mathrm{d}{\rho }^{\prime}\end{array}\right].\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq17.gif) (14)
(14)
The integrals of 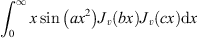 and
and 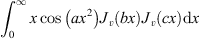 [18], and the formula J
−m
(x) = (−1)m
J
m
(x) are used in deriving equation (14).
[18], and the formula J
−m
(x) = (−1)m
J
m
(x) are used in deriving equation (14).![$$ {\int }_0^{\infty }x\mathrm{sin}\left(a{x}^2\right){J}_v\left({bx}\right){J}_v({cx})\mathrm{d}x=\frac{1}{2a}\mathrm{cos}\left(\frac{{b}^2+{c}^2}{4a}-\frac{v}{2}\pi \right){J}_v\left(\frac{{bc}}{2a}\right)[a>0,b>0,c>0,\mathfrak{R}{ev}>-2] $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq20.gif) (15)
(15)
![$$ {\int }_0^{\infty }x\mathrm{cos}\left(a{x}^2\right){J}_v\left({bx}\right){J}_v({cx})\mathrm{d}x=\frac{1}{2a}\mathrm{sin}\left(\frac{{b}^2+{c}^2}{4a}-\frac{v}{2}\pi \right){J}_v\left(\frac{{bc}}{2a}\right)[a>0,b>0,c>0,\mathfrak{R}{ev}>-1] $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq21.gif) (16)
(16)
![$$ \begin{array}{c}U\left(\rho,\theta,z\right)=-\frac{{ik}}{f}\mathrm{exp}\left[{ik}\left(z+\frac{{v}_0^2}{2f}-\frac{{{zv}}_0^2}{{f}^2}-\frac{{\rho }^2}{2z}\right)\right]{v}_0\\ \left\{{c}_0{J}_0\left(\frac{k}{f}\rho {v}_0\right)+\sum_{m=-\infty }^{\infty }{\left(-i\right)}^m\left[{c}_m\mathrm{exp}\left({im\theta }\right)+{c}_{-m}\mathrm{exp}\left(-{im\theta }\right)\right]{J}_m\left(\frac{k}{f}\rho {v}_0\right)\right\}.\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq22.gif) (17)
(17)
To generate nondiffracting radial carpet-lattice beams, we choose a radial amplitude grating with a sinusoidal transmission function [1]:![$$ t\left(\phi \right)=A\left(\phi \right)=\frac{1}{2}\left[1+\mathrm{cos}\left({m\phi }\right)\right]=\frac{1}{2}+\frac{1}{4}\left({e}^{{im\phi }}+{e}^{-{im\phi }}\right), $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq23.gif) (18)where m is the number of spokes of the grating.
(18)where m is the number of spokes of the grating.
We can obtain c
0 = 1/2, c
m
= c
−m = 1/4 and c
n≠m = 0 by comparing equations (2) and (17). We then substitute the coefficients into equation (17). The distribution of the resulting light field is given as:![$$ \begin{array}{c}U(\rho,\theta,z)=-\frac{{ik}}{2f}\mathrm{exp}\left[{ik}\left(z+\frac{{{v}_0}^2}{2f}-\frac{z{{v}_0}^2}{{f}^2}-\frac{{\rho }^2}{2z}\right)\right]{v}_0\\ \times \left\{{J}_0\left(\frac{k}{f}\rho {v}_0\right)+{\left(-i\right)}^m\mathrm{cos}\left({m\theta }\right){J}_m\left(\frac{k}{f}\rho {v}_0\right)\right\}.\end{array} $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq24.gif) (19)
(19)
The intensity distribution of the light field at distance z can be calculated as I(ρ, θ, z) = U(ρ, θ, z) · U*(ρ, θ, z), where * denotes a complex conjugate. Hence, we can obtain:![$$ I\left(\rho,\theta,z\right)=\frac{{k}^2{{v}_0}^2}{4{f}^2}\left\{\left[{\left(-i\right)}^m+{(i)}^m\right]\mathrm{cos}\left({m\theta }\right){J}_0\left(\frac{k}{f}\rho {v}_0\right){J}_m\left(\frac{k}{f}\rho {v}_0\right)+{{J}_0}^2\left(\frac{k}{f}\rho {v}_0\right)+{\mathrm{cos}}^2\left({m\theta }\right){{J}_m}^2\left(\frac{k}{f}\rho {v}_0\right)\right\}. $$](/articles/jeos/full_html/2025/02/jeos20250028/jeos20250028-eq25.gif) (20)
(20)
Equation (17) shows that our constructed radial carpet-lattice beams are propagation-invariant because the propagating distance z does not appear in the argument of the Bessel function J 0 and J m . The optical distribution of radial carpet-lattice beams is always the same for different propagating distances z. On the basis of equation (20), we typically simulate several types of nondiffracting radial carpet-lattice beams with different parameters in MATLAB, as shown in Figure 1. Noted that all simulated subgraphs in Figure 1 share the same color bars. Figure 1 shows that the lattice characteristics of nondiffracting radial carpet-lattice beams are different when the number of spokes m of the radial grating is odd and even. From equation (20), [(−i)m + (i)m ] is always 0 when m is odd. When m is even, there is [(−i)m + (i)m ] = ±2. These results indicate that the optical structures of odd and even order nondiffracting radial carpet-lattice beams are fundamentally different. As shown in Figure 1, the m-order radial carpet-lattice beams have m spokes for the radial grating with even number of spokes. Figure 1 shows that as the spokes of m increases, the carpet beam becomes increasingly close to the lattice structure, which is the reason for naming it as the carpet-lattice beam. For the radial grating with odd number of spokes, the m-order radial carpet beams have 2m spokes, thereby exhibiting fundamentally different from even order radial carpet-lattice beams. These different lattice properties may lead to new different uses.
 |
Figure 1 Simulation graph of the nondiffracting radial carpet-lattice beams generated by the diffraction of radial gratings with multiple odd and even spoke numbers m. |
3 Experiment
To generate the nondiffracting radial carpet-lattice beams, we had to extend the original Durnin’s setup into a new experimental system, as shown in Figure 2. An amplitude-type SLM is an important element to be used as amplitude modulation. Hence, in our experimental system, the annular pupil aperture with arbitrary azimuthal amplitude components is loaded into the SLM. He-Ne laser source (632.8 nm) is initially expanded. The collimating parallel laser is incident on the amplitude-type SLM (GC-SLM-T-XGA, 22 μm pixel size, 1080 × 768 pixels). The SLM resides in the front focal plane of Fourier transform lens with focal length f = 40 cm. The nondiffracting radial carpet-lattice beams can be generated after the Fourier transform lens. In our work, we load the spectrum information of nondiffracting radial carpet-lattice beams on an annular slit with a diameter of 10 mm and a width of 350 μm, as shown in Figure 3. The polarizers are introduced to adjust the incident light to the working polarization state of the SLM, ensuring the optimal amplitude modulation effect. Additionally, it can filter out non-target polarized light to improve the purity of the light beam. The nondiffracting radial carpet-lattice beams are generated and recorded by using a scientific charge-coupled device camera (Microvision 130FC, pixel unit size of 5.4 μm), as shown in Figure 4. Figure 4 shows that the recorded experimental diffraction patterns of the annular slit of radial grating are consistent with the theoretical predictions. Compared Figure 4 with Figure 1, the radial carpet-lattice beams generated by the diffraction of radial gratings with different spoke numbers exhibit shapes that are largely consistent with those simulated by equation (20). Nondiffracting radial carpet-lattice beams of odd and even orders show distinct shape characteristics. Nondiffracting carpet-lattice beams possess peculiar central radiating optical lattice structures, serving as potential tools for advanced applications such as manufacturing photonic crystal fibers, optical trap for cold atoms or molecules, Bose-Einstein condensation of particle, sub-Doppler cooling, quantum computation, delocalized entanglement of atoms, and so on.
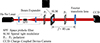 |
Figure 2 The experimental system for generating nondiffracting radial carpet-lattice beams based on extended Durnin’s experimental setup. |
 |
Figure 3 Annular slits with radial grating information for different parameters. |
 |
Figure 4 Experimental graph of nondiffracting radial carpet-lattice beams with the same parameters as in Figure 1. |
The nondiffracting beams are theoretical pattern instead of a physically realizable entity since they are characterized as carrying infinite energy and having an infinite extent. However, any actual physical beam is limited by the finite aperture of optical systems (such as the size of spatial light modulators, the radial range of gratings, etc.). Therefore, the radial carpet-lattice beam generated in experiments is essentially a pseudo-nondiffracting approximation, with a finite lattice depth and a truncated spectral distribution, and its nondiffracting characteristics are only valid within a finite propagation distance. Nevertheless, the beam can still exhibit a highly stable periodic intensity distribution within the preset propagation range, providing a feasible approximate solution for applications such as optical manipulation and particle trapping. On the basis of the experimental parameter, the maximum nondiffraction distance is obtained from the formula z max = R/tanθ, where tanθ ≈ d/2f, R is the finite output aperture, d is the annular slit with a diameter of 10 mm, here, f refers to the focal distance of the Fourier lens [5]. Therefore, we calculate the ideal maximum transmission distance as 400 cm.
We verify the nondiffracting transmission characteristics of the generated radial carpet-lattice beams in the range of z < z max. Taking the radial carpet-lattice beam with m = 9 as an example, a charge-coupled device camera is used to record the intensity distribution in different propagation distances after the Fourier lens, as shown in Figure 5. The experimental results indicate that the radial carpet-lattice beams generated by the Durnin’s setup is an approximate nondiffracting beam, it maintaining basically unchanged shape and size, with only slight changes in light intensity in the range of z < z max. Hence the method to generate nondiffracting radial carpet-lattice beams based on the Durnin’s setup is feasible.
 |
Figure 5 Recorded graphs of nondiffracting radial carpet-lattice beams for parameter m = 9 at different propagation distances after the lens: (a) z = 50 cm; (b) z = 80 cm; (c) z = 110 cm; (d) z = 140 cm; (e) z = 170 cm. |
4 Conclusion
We propose a generating method of nondiffracting radial carpet-lattice beams using an extended version of Durnin’s experimental setup. We first establish the theoretical framework for constructing nondiffracting radial carpet-lattice beams. By loading the annular slit containing the transmission function information of radial gratings onto the SLM, a series of nondiffracting radial carpet-lattice beams were obtained on the plane behind the Fourier transform lens, the analytical expression for their optical field distribution is derived. We typically record several types of nondiffracting radial carpet-lattice beams by loading the annular slit with the radial grating transmission function information on the amplitude-type SLM. Experimental results verify the theoretical predictions, validating that the SLM-aided Durnin’s experimental setup is an effective method to generate radial carpet-lattice beams with nondiffracting propagation. Furthermore, the similar setup can be adopted to generate other types of nondiffracting combined half-integer Bessel-like beams.
Funding
This work was supported by National Natural Science Foundation of China (No. 62475240).
Conflicts of interest
The authors declare no conflict of interest in regards to this article.
Data availability statement
This article has no associated data generated and/or analyzed/Data associated with this article cannot be disclosed due to legal/ethical/other reason.
Author contribution statement
Conceptualization, Ning Gong and Zhijun Ren; Methodology, Zhijun Ren; Software, Ning Gong,Yefeng Liu and Bo Zhang; Validation, Youxiang Ye, Changjiang Fan and Zhijun Ren; Formal Analysis, Ning Gong and Zhijun Ren; Writing – Original Draft Preparation, Ning Gong; Writing – Review & Editing, Ning Gong and Zhijun Ren; Project Administration, Ning Gong and Zhijun Ren.
References
- Hebri D, Rasouli S, Combined half-integer bessel-like beams: a set of solutions of the wave equation, Phys. Rev. A. 98, 4 (2018). https://doi.org/10.1103/PhysRevA.98.043826. [Google Scholar]
- Rasouli S, Khazaei AM, Hebri D, Talbot carpet at the transverse plane produced in the diffraction of plane wave from amplitude radial gratings, J. Opt. Soc. Am. A. 35, 1 (2018). https://doi.org/10.1364/JOSAA.35.000055. [Google Scholar]
- Rasouli S, Khazaei AM, Hebri D, Radial carpet beams: a class of nondiffracting, accelerating, and self-healing beams, Phys. Rev. A. 97, 3 (2018). https://doi.org/10.1103/PhysRevA.97.033844. [Google Scholar]
- Liu Y, Li H, Chen R, Fan C, Shi Y, Ren Z, Non-diffracting integer-order and half-integer-order carpet beams obtained by even-type sinusoidal amplitude radial gratings, Chin. Opt. Lett. 22, 7 (2024). https://doi.org/10.3788/col202422.072601. [Google Scholar]
- Durnin J, Miceli JJ, Eberly JH, Diffraction-free beams, Phys. Rev. Lett. 58, 15 (1987). https://doi.org/10.1103/PhysRevLett.58.1499. [Google Scholar]
- McGloin D, Dholakia K, Bessel beams: diffraction in a new light, Contemp. Phys. 46, 1 (2005). https://doi.org/10.1080/0010751042000275259. [Google Scholar]
- Vasilyeu R, Dudley A, Khilo N, Forbes A, Generating superpositions of higher-order Bessel beams, Opt. Express. 17, 26 (2009). https://doi.org/10.1364/OE.17.023389. [Google Scholar]
- Gutiérrez-Vega JC, Iturbe-Castillo MD, Tepichin E, Ramírez GA, Rodriguez-Dagnino RM, Châvez-Cerda SC, New member in the family of propagation-invariant optical fields: Mathieu beams, Opt. Photonics. News. 11, 12 (2000). https://doi.org/10.1364/OPN.11.12.000037. [Google Scholar]
- Ren Z, He J, Shi Y, Generation of Mathieu beams using angular pupil modulation, Chin. Phys. B. 27, 12 (2018). https://doi.org/10.1088/1674-1056/27/12/124201. [Google Scholar]
- Gutiérrez-Vega JC, Iturbe-Castillo MD, Chávez-Cerda S, Alternative formulation for invariant optical fields: Mathieu beams, Opt. Lett. 25, 20 (2000). https://doi.org/10.1364/OL.25.001493. [Google Scholar]
- Bandres MA, Gutiérrez-Vega JC, Chávez-Cerda S, Parabolic nondiffracting optical wave fields, Opt. Lett. 29, 1 (2004). https://doi.org/10.1364/OL.29.000044. [Google Scholar]
- López-Mariscal C, Bandres MA, Gutiérrez-Vega JC, Chávez-Cerda S, Observation of parabolic nondiffracting optical fields, Opt. Express 13, 7 (2005). https://doi.org/10.1364/OPEX.13.002364. [Google Scholar]
- Davis J A, Carcole E, Cottrell D M, Nondiffracting interference patterns generated with programmable spatial light modulators, Appl. Opt. 35, 4 (1996). https://doi.org/10.1364/ao.35.000599. [Google Scholar]
- Bowman R, Muller N, Zambrana-Puyalto X, Jedrkiewicz O, Di Trapani P, Padgett M J, Efficient generation of Bessel beam arrays by means of an SLM, Eur. Phys. J. Spec. Top. 199, 159 (2011). https://doi.org/10.1140/epjst/e2011-01511-3. [Google Scholar]
- Latychevskaia T, Schachtler D, Fink H W, Creating Airy beams employing a transmissive spatial light modulator, Appl. Opt. 55, 22 (2016). https://doi.org/10.1364/ao.55.006095. [Google Scholar]
- Bouchal Z, Nondiffracting optical beams: physical properties, experiments and applications, Czech. J. Phys. 53, 7 (2003). https://doi.org/10.1023/A:1024802801048. [Google Scholar]
- Arfken GB, Mathematical Methods for Physicists, 3rd edn. (Academic Press, 1985). [Google Scholar]
- Gradshteyn IS, Ryzhik IM, Table of Integrals, Series, and Products (Academic Press, 2007). [Google Scholar]
All Figures
 |
Figure 1 Simulation graph of the nondiffracting radial carpet-lattice beams generated by the diffraction of radial gratings with multiple odd and even spoke numbers m. |
| In the text | |
 |
Figure 2 The experimental system for generating nondiffracting radial carpet-lattice beams based on extended Durnin’s experimental setup. |
| In the text | |
 |
Figure 3 Annular slits with radial grating information for different parameters. |
| In the text | |
 |
Figure 4 Experimental graph of nondiffracting radial carpet-lattice beams with the same parameters as in Figure 1. |
| In the text | |
 |
Figure 5 Recorded graphs of nondiffracting radial carpet-lattice beams for parameter m = 9 at different propagation distances after the lens: (a) z = 50 cm; (b) z = 80 cm; (c) z = 110 cm; (d) z = 140 cm; (e) z = 170 cm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


