EDP Sciences logo
Submit your research paper
Search
Menu
All issues Volume 21 / No 2 (2025) J. Eur. Opt. Society-Rapid Publ., 21 2 (2025) 38 Full HTML
Open Access
Issue
J. Eur. Opt. Society-Rapid Publ.
Volume 21, Number 2, 2025
Article Number 38
Number of page(s) 8
DOI https://doi.org/10.1051/jeos/2025033
Published online 11 August 2025

© The Author(s), published by EDP Sciences, 2025

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

In recent decades, generation ultrashort optical pulses with single or even subcycle, has been regarded as a basic optical topic, shows great progresses in the range of THz, visible and extreme ultraviolet band [1–5] as ultrafast optical pulses, with few-, single- or sub-cycle, they are used for coherent population transfer, because they can easily access to the electric ground states of many molecules. Especially in the multi-level system, the single- and sub-cycle pulses show more suitable application for transferring population due to their ultrabroad spectra [6]. Various techniques for generation ultrafast pulse have been proposed and studied in both theory and experiment [7–12]. And the bandwidths of the experimental pulses have reached several or even tens of THz [13]. Among these excellent works, the spontaneous parametric down conversion (SPDC) is a primary and convenient method for generating biphotons with entanglement [14–18].

The SPDC process mainly concerns the interaction between the pump light and the nonlinear crystal. The crystal is precisely designed for SPDC, such as periodically poled lithium niobate (PPLN) in this paper. As the pump light with frequency ω p incidents into this crystal, it can be split into two photons named as signal and idler lights with lower frequencies ω s and ω i, respectively. The two simultaneously generated photons show wide broadband spectra and high degree of entanglement based on the squeezed quantum states. Generally, the broadband spectra could be produced by a thin nonlinear crystal. And the spectra bandwidth is inversely proportional to the length of crystal during SPDC [19, 20]. However, the effect produced by shortening the crystal length to increase the spectral width is limited. The bandwidth of the biphotons can be made wider by other methods, such as the more perfect phase-matching condition [21], the better phase compensation [22], or chirped quasi-phase-matched crystals [23], etc.

The collinear SPDC is an ideal model for the generation of ultrafast biphotons with single cycles. However, in experiments, two factors need to be considered: the effect of temperature on the crystal length and the effect of angle on the noncollinear SPDC. Reference [24] focused on the thermal expansion and contraction effect of temperature on nonlinear crystals, which directly determines the effect of temperature on the grating periods of the QPM PPLN crystal. Reference [25] focused on the effect of angle on the SPDC, and found that a single cycles ultrashort pulse can be generated with tiny angle.

In this paper, we focus on the chirped QPM PPLN crystal, it is subjected to the influence of thermal expansion and contraction in SPDC process, which affects the optical path of pulse propagation in the crystal [26], and this directly determines other characteristics for the biphotons. Especially for QPM crystal, where thermal effects can change the period of nonlinear crystals and thus alter the phase matching conditions. Given this, we consider the influence of crystal’s thermal expansion and contraction effect on chirp QPM, and explore its impact on the biphotons characteristics generated by SPDC. In the noncollinear SPDC, temperature plays an important role in the whole process, especially the influence on the grating periods of the QPM crystal and the angle of noncollinear process. Both the two factors determine the effectiveness of phase matching. Therefore, we focus on the effect of temperature modulation on the grating periods in chirped quasi-phase-matched crystal and the effect of angle in the noncollinear process, so that it is help to generate the ultrashort pulses with narrower temporal width in experiments.

2 Theory

2.1 The noncollinear SPDC in chirped QPM PPLN

In SPDC, the pump light incidents into the chirped QPM PPLN crystal and split into two photons named signal and idler lights. As we consider the type 0 (e → e + e), the pump, signal and idler photons are extraordinary lights, they can be expressed by creation and annihilation operators during SPDC process [27]: E μ e ̂ ( r , t ) = i 2 π ∫ [ | n e ( k ) | - 1 ( hν ) 1 / 2 a ̂ eμ † ( k ) e ikr - iω t e ̂ ( k ) ] d k + [ | n e ( k ) | - 1 ( hν ) 1 / 2 a ̂ eμ ( k ) e ikr + iω t e ̂ ( k ) ] d k , $$ {E}_{\mu \hat{e}}\left(r,t\right)=\frac{i}{2\pi }\int \left[{\left|{n}_e(k)\right|}^{-1}{\left({h\nu }\right)}^{1/2}{\hat{a}}_{{e\mu }}^{\dagger }(k){e}^{{ikr}-{i\omega t}}\hat{e}(k)\right]\mathrm{d}k+\left[{\left|{n}_e(k)\right|}^{-1}{\left({h\nu }\right)}^{1/2}{\hat{a}}_{{e\mu }}(k){e}^{{ikr}+{i\omega t}}\hat{e}(k)\right]\mathrm{d}k, $$(1)where μ = p, s, i represent pump, signal and idler lights. 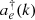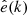a e † ( k ) $ {a}_e^{\dagger }(k)$ and a e ( k ) $ {a}_e(k)$ are the creation and annihilation operators in the poled vectors e ̂ ( k ) $ \hat{e}(k)$ for extraordinary lights. For simplicity, it is assumed that the pump light as a monochromatic one with central wavelength λ p = 0.42 μm, and its frequency signed as ω p [23]. Its electric field is independent with time and expressed as: E p = ∫ E p 0 δ ( ω - ω p ) d ω . 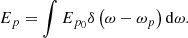$$ {E}_p=\int {E}_{{p}_0}\delta \left(\omega -{\omega }_p\right)\mathrm{d}{\omega }. $$(2)

As the pump light propagates in a general nonlinear crystal, the down conversion efficiency would be decreased. JA Armstrong et al. [28] have proposed a method called the quasi-phase-matching (QPM). It is designed as periodically poled grating with alternate reversal poled directions. 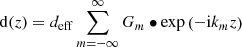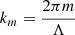These poled gratings in QPM can be expressed with Fourier expansion forms shown as follows [29]: d ( z ) = d eff ∑ m = - ∞ ∞ G m ∙ exp ( - i k m z ) $$ \mathrm{d}(z)={d}_{\mathrm{eff}}\sum_{m=-\infty }^{\infty }{G}_m\bullet \mathrm{exp}\left(-\mathrm{i}{k}_mz\right) $$(3)where d eff is the effective nonlinear coefficient for the nonlinear crystal, and k m = 2 π m Λ $ {k}_m=\frac{2{\pi m}}{\mathrm{\Lambda }}$ is the mth Fourier form for the grating vector.

For PPLN crystal, its length is also affected by thermal expansion and cold contraction, which can be expressed by the temperature dependent thermal expansion and cold contraction formula shown as follows [24]: L ( T ) = L 0 [ 1 + β ( T ) ( T - T 0 ) ] , $$ L(T)={L}_0\left[1+\beta (T)\left(T-{T}_0\right)\right], $$(4)where L 0 is the crystal length when T 0 = 25 °C, β(T) is the thermal expansion coefficient. The crystal length increases in approximately positive proportion with the increase of temperature. Meanwhile, the grating poled period along the propagation direction is also affected by thermal expansion and cold contraction, and its change can also be expressed by the above equation. In generally, the total crystal length is the sum of the length of each poled grating period Λ j (T), which can be expressed by the following equation: L ( T ) = Λ 0 + Λ 1 + Λ 2 + … = ∑ j Λ j ( T ) . 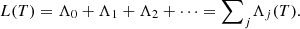$$ L(T)={\mathrm{\Lambda }}_0+{\mathrm{\Lambda }}_1+{\mathrm{\Lambda }}_2+\dots ={\sum }_j{\mathrm{\Lambda }}_j(T). $$(5)

Consider the chirped QPM PPLN crystal as shown in Figure 1, each poled grating period is a function of the propagation direction z. For the sake of convenience, let’s assume that the grating periods in this crystal are linearly varying, with reversal directions in the adjacent bulks shown in Figure 1. And the spatial grating vector K(z) can be expressed by the chirped poled grating periods: K ( z ) = 2 π Λ ( z ) = K 0 - ζ z , $$ K(z)=\frac{2\pi }{\mathrm{\Lambda }(z)}={K}_0-{\zeta z}, $$(6)where K 0 is selected for the perfect phase matching determined by the first grating period Λ0 in the left edge of the nonlinear crystal. It can be perfectly phase matched with the incident pump light. The modulation of the grating periods Λ(z) for the chirped QPM PPLN crystal is linearly varying along the propagation direction. The latter chirped poled grating periods matches the phases mismatching of the biphotons generated by SPDC.

thumbnail Fig. 1

Scheme of noncollinear SPDC in chirped QPM PPLN crystal. The directions of arrows in the crystal represent polarized axis for the QPM PPLN crystal. The pump, signal and idler lights are denoted by p, s, i respectively.

As the pump light propagates in the chirped QPM crystal, the spatial phase ϕ(z) caused by the chirped QPM with the chirp rate ζ can be accumulated as follows: ϕ ( z ) = ∫ ζ z d z = ζ z 2 2 . $$ \phi (z)=\int {\zeta z}\mathrm{d}z=\frac{{{\zeta z}}^2}{2}. $$(7)

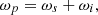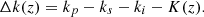In the three mixed waves process of SPDC, the angular momentum relation and the phase mismatching relation can be shown as follows: ω p = ω s + ω i , $$ {\omega }_p={\omega }_s+{\omega }_i, $$(8) Δ k ( z ) = k p - k s - k i - K ( z ) . $$ \Delta k(z)={k}_p-{k}_s-{k}_i-K(z). $$(9)

Equation (7) is applied to the special case of monochromatic pump. And the phase mismatching Δk for the three waves in equation (8) plays a significant role in the SPDC, which determines the parametric gain and the efficiency of the conversion [30]. As we consider the monochromatic pump could split into two new photons, and the biphotons can propagate along the nonlinear crystal with the angle of θ relative to the pump photon during the noncollinear SPDC process. In the case of collinear (θ = 0) SPDC, the biphotons are generated in the same optical mode and separated by the frequency filter during the propagation through two independent paths. And in the case of noncollinear (θ ≠ 0) SPDC, the generated biphotons could pass in different optical path by themselves without the help of frequency filter.

In noncollinear SPDC, the signal and idler photons propagate through the nonlinear crystal with the angle θ relative to the pump propagation direction. The process satisfies the energy and momentum conservations. The phase mismatching Δk in equation (8) can be modified as follows [25, 31]: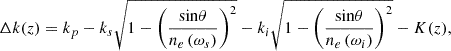 Δ k ( z ) = k p - k s 1 - ( sin θ n e ( ω s ) ) 2 - k i 1 - ( sin θ n e ( ω i ) ) 2 - K ( z ) , $$ \Delta k(z)={k}_p-{k}_s\sqrt{1-{\left(\frac{\mathrm{sin}\theta }{{n}_e\left({\omega }_s\right)}\right)}^2}-{k}_i\sqrt{1-{\left(\frac{\mathrm{sin}\theta }{{n}_e\left({\omega }_i\right)}\right)}^2}-K(z), $$(10)where 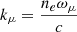k μ = n e ω μ c $ {k}_{\mu }=\frac{{n}_e{\omega }_{\mu }}{c}$ (μ = p, s, i) represent the wave vectors of pump, signal and idler photons for extraordinary lights. The angle θ of noncollinear has been demonstrated in Ref. [25] in theory and verified in experiment with the range of ±0.25±0.14 degree.

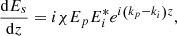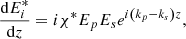According to equation (1), the general coupling equations for the three mixed waves can be written as [29]: d E s d z = i χ E p E i * e i ( k p - k i ) z , $$ \frac{\mathrm{d}{E}_s}{\mathrm{d}z}=i\mathrm{\chi }{E}_p{E}_i^{*}{e}^{i\left({k}_p-{k}_i\right)z}, $$(11) d E i * d z = i χ * E p E s e i ( k p - k s ) z , $$ \frac{\mathrm{d}{E}_i^{*}}{\mathrm{d}z}=i{\mathrm{\chi }}^{*}{E}_p{E}_s{e}^{i\left({k}_p-{k}_s\right)z}, $$(12)where χ is a three wave coupling constants. According to equation (10) and equation (11) and the spatial phase ϕ(z) in equation (6) with quadratic factor, the three mixed waves equations in the chirped QPM PPLN crystal can be formed as follows [23]: ∂ A s ∂ z = iξ ( z ) A i * exp [ iϕ ( z ) + i Δ k*z ] , $$ \frac{\mathrm{\partial }{A}_s}{\mathrm{\partial }z}={i\xi }(z){A}_i^{*}\mathrm{exp}\left[{i\phi }(z)+i\Delta {k*z}\right], $$(13) ∂ A i * ∂ z = - i ξ * ( z ) A s exp [ - iϕ ( z ) - i Δ k*z ] , $$ \frac{\partial {A}_i^{*}}{{\partial z}}=-i{\xi }^{*}(z){A}_s\mathrm{exp}\left[-{i\phi }(z)-i\Delta {k*z}\right], $$(14)where ξ(z) consists of the factors of pump spectral amplitude, nonlinear crystal refractive index, and nonlinear effective coefficient. It is quite slowly varying as the changing of the frequency and positions. So ξ(z) can be simply regarded as χ in equation (11) and equation (12). The coupling interaction shown in equation (13) is mainly concerns two factors: the phase mismatching function Δk and the spatial phase ϕ(z).

According to equation (7), the frequencies of signal and idler photons can be written as ω and ω p − ω, respectively. Considering the temperature and angle influence, the form of the biphotons state function can be expressed as: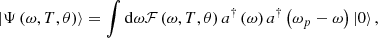 | Ψ ( ω , T , θ ) 〉 = ∫ d ω F ( ω , T , θ ) a † ( ω ) a † ( ω p - ω ) | 0 〉 , $$ \left|\mathrm{\Psi }\left(\omega,T,\theta \right)\right\rangle=\int \mathrm{d}\omega \mathcal{F}\left(\omega,T,\theta \right)\right.{a}^{\dagger }\left(\omega \right){a}^{\dagger }\left({\omega }_p-\omega \right)\left|0\right\rangle\right., $$(15)where 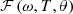F ( ω , T , θ ) $ \mathcal{F}\left(\omega,T,\theta \right)$ is the joint spectral amplitude function. 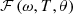By integrating over the entire length of the crystal, the spectrum for this process can be expressed as follows [23]: F ( ω , T , θ ) ∼ exp [ - i Δ k ( ω , T , θ ) 2 ζ ] × { erfi [ ( 1 + i ) Δ k ( ω , T , θ ) 2 ζ ] - erfi [ ( 1 + i ) ( Δ k ( ω , T , θ ) + ζ L ( T ) ) 2 ζ ] } , $$ \mathcal{F}\left(\omega,T,\theta \right)\sim \mathrm{exp}\left[-i\frac{\Delta k\left(\omega,T,\theta \right)}{2\zeta }\right]\times \left\{\mathrm{erfi}\left[\frac{\left(1+i\right)\Delta k\left(\omega,T,\theta \right)}{2\sqrt{\zeta }}\right]-\mathrm{erfi}\left[\frac{\left(1+i\right)\left(\Delta k\left(\omega,T,\theta \right)+{\zeta L}(T)\right)}{2\sqrt{\zeta }}\right]\right\}, $$(16)where erfi is an imaginary error function. Nearly all the spectral/temporal properties are determined by the joint spectral amplitude function F ( ω , T , θ ) $ \mathcal{F}\left(\omega,T,\theta \right)$. Such as the squared module 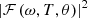| F ( ω , T , θ ) | 2 $ {\left|\mathcal{F}\left(\omega,T,\theta \right)\right|}^2$ can be viewed as the spectral function.

2.2 The characteristics of the biphotons and the pulse compression

In general, the given biphotons with a broad spectrum does not mean it has a ultrashort temporal width. Caused by quadratic phase matching, the way of producing the temporal wave function in QPM is not Fourier transform limited [32, 33]. However, the converse one is correct. That the biphotons with shorter temporal width is necessarily mean it has a broader frequency spectrum [32]. Thus, the chirped QPM SPDC indicates that biphotons can be generated with a broad bandwidth and can be compressed into a shorter temporal pulse with phase compensation. To compress the chirped biphotons generated by SPDC, Harris has proposed a perfect phase compensation method with Fourier transform limit [23]. And the biphotons with a single cycle can be detected by homodyning detection. It is viewed as an ideal pulse which can be used to probe the quantum optical properties.

When the pump light is a monochromatic one, according to the angular momentum relation shown in equation (7), we can obtain the count rate (CT) of the entangled biphotons generated by the chirped QPM PPLN crystal in noncollinear SPDC as follows: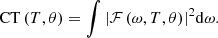 CT ( T , θ ) = ∫ | F ( ω , T , θ ) | 2 d ω . $$ \mathrm{CT}\left(T,\theta \right)=\int {\left|\mathcal{F}\left(\omega,T,\theta \right)\right|}^2\mathrm{d}\omega. $$(17)

Of course, the count rate of biphotons can also be calculated by the representation of the second-order Glauber intensity correlation. The bandwidth (BW) of the generated biphotons can be obtained based on the center frequency. We can calculate the specific spectral bandwidth according to the following formula: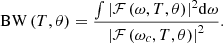 BW ( T , θ ) = ∫ | F ( ω , T , θ ) | 2 d ω | F ( ω c , T , θ ) | 2 . $$ \mathrm{BW}\left(T,\theta \right)=\frac{\int {\left|\mathcal{F}\left(\omega,T,\theta \right)\right|}^2\mathrm{d}\omega }{{\left|\mathcal{F}\left({\omega }_c,T,\theta \right)\right|}^2}. $$(18)

It can be calculated that the bandwidth of the biphotons generated by SPDC in the chirped QPM PPLN crystal reaches the THz level.

As the ultrabroad biphotons have be generated in the chirped QPM PPLN crystal, we would like to quantitative analysis the correlation of biphotons. In order to compress the temporal width of the biphotons, we should make the broadband in frequency domain be transferred into temporal domain with Fourier transform limit. In Ref. [23], it is proposed a method that the quadratic mismatching phase can be compensated by the function shown as [23]: CF = exp [ i ( Δ k 2 2 ζ ) - i ( k s + k i ) L ] . $$ \mathrm{CF}=\mathrm{exp}\left[i\left(\frac{{\Delta k}^2}{2\zeta }\right)-i\left({k}_s+{k}_i\right)L\right]. $$(19)

In collinear SPDC, signal and idler photons can be generated with wider bandwidth. They can be separated by filter and propagate through their own path in the dispersive compensation media. With the help of the CF function shown in equation (18), the signal and idler photons generated in the chirp QPM in SPDC, could be compensated when they propagate through their own paths. One channel is compensated by the dispersion function, the other is modulated by the experimental time delay. They can simultaneously arrive at the ultrafast correlator [34] and generate sum frequency pulse. It can detect the single cycle biphotons by homodyning detection between the sum frequency and pump frequency which are equal to each other. But in the noncollinear SPDC, the filter is no longer needed to separate the two photons. For there is already an angle between the two photons propagation paths. However, Fourier transformation can be used to transform the spectral power of the biphotons into the time domain expression. And the single cycle biphotons could be detected by homodyning detection [23].

3 Temperature dependent phase mismatching

For the first order QPM generation in collinear, the temperature shows weakly influence in SPDC (e → e + e) [29]. The temperature influence to refractive index can be described by Sellmeier equation [35–38]. In this equation, the refractive index for PPLN crystal can be described as follows [36]: n 2 = A 1 + A 2 + B 1 R λ 2 - ( A 3 + B 2 R ) 2 + B 3 R - A 4 λ 2 , $$ {n}^2={A}_1+\frac{{A}_2+{B}_1R}{{\lambda }^2-{\left({A}_3+{B}_2R\right)}^2}+{B}_3R-{A}_4{\lambda }^2, $$(20)where λ is the vacuum wavelength in microns and A 1, A 2, A 3, B 1, B 2 and B 3 are all constants shown in Ref. [35]. R is a temperature dependent function for lithium niobate, expressed as R(T) = (T − T 0) (T + T 0 + 546), where T 0 = 24.5 °C and T is the temperature in centigrade. For the congruent lithium niobate, the temperature dependent Sellmeier equation can be reduced by [36]: n 2 = A 1 + A 2 λ 2 - A 3 2 - A 4 λ 2 $ {n}^2={A}_1+\frac{{A}_2}{{\lambda }^2-{A}_3^2}-{A}_4{\lambda }^2$. Furthermore, this equation has been improved by Jundt [37] for congruent lithium niobite. These improvements for Sellmeier equation help us make accurate simulation for the refractive index of PPLN and apply to the chirped QPM SPDC. The adjustable refractive index n e for extraordinary photon is related with the temperature in Sellmeier equation, so phase-mismatched wave-vector Δk is a temperature dependent function. The phase matching effect can be influenced by the refractive index with different temperatures.

Firstly, it can be seen from equation (15) that the joint spectral amplitude function is mainly determined by the phase mismatching function Δk, and is also limited by the chirp rate ζ and crystal length L. The frequency response range is mainly affected by the following equation: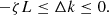 - ζ L ≤ Δ k ≤ 0 . $$ -{\zeta L}\le \Delta k\le 0. $$(21)

For comparison the influence of the phase mismatching function caused by the different angles, Figure 2 shows the distribution of the phase mismatching function versus the temperature and frequency with the angle of θ = 0.06 deg and θ = 0.16 deg. It can find that when angle is small (e.g. θ = 0.06 deg), the phase mismatching function would show wide frequency range in –ζL ≤ Δk ≤ 0. It also indicates that the phase matching effect with θ = 0.06 deg is better than that of θ = 0.16 deg. It can be viewed as a fundamentally reason for the relevant conclusions in this paper.

thumbnail Fig. 2

The ∆k/ζL versus temperature and frequency with (a) θ = 0.06 deg; (b) θ = 0.16 deg.

It can be seen from Figure 2 that when the angle θ is small, the frequency response range of the phase matching function Δk shows wider range satisfying equation (20). With the increasing of the angle θ, the effect of phase matching gradually decreases. Such as the examples shown in Figure 2, there are more frequencies near the central frequency ω p/2 corresponding to the phase mismatching function tends to zero with the angle (θ = 0.06 deg).

4 Simulation and discussion

The count rate and the bandwidth of the generated biphotons can be calculated according to equation (16) and equation (17). As shown in Figure 3a, the count rate of biphotons generated in noncollinear SPDC with deterministic angle would decrease as the temperature increases. For different angles, these plot lines are almost parallel to each other in Figure 3a. Meanwhile, the speed of decreasing would be quicker as the angle θ increases with the same temperature range. This property is consistent with the physical expectation that the count rate would be decrease as the temperature increases in the noncollinear SPDC. A similar conclusion can be obtained from Figure 3b that the bandwidth of the biphotons would be narrowed as the temperature increases in noncollinear SPDC with deterministic angle. And the bandwidth of the biphotons would be obviously narrower as the angle θ becomes bigger. We can find that the plot dots density becomes much thinner with larger angle in this figure. These two graphs in Figure 3 show similar distributions with the varying of temperature for the same angles. It is because that they are both determined by the phase mismatching function Δk.

thumbnail Fig. 3

(a) The count rate and (b) the bandwidth of biphotons versus the temperature for different angles θ.

It can be concluded from the Figures 2 and 3 that the biphotons with many properties are closely related to the angle θ, and influenced by the temperature. They are mainly determined by the phase mismatching function Δk. The smaller angle, and the lower temperature (such as room temperature) make the phase matching be more perfect. Here, we set θ = 0.06 deg and θ = 0.16 deg with temperature T = 25 °C, and draw the figures of sum power and homodyne current according to the method shown in Ref. [25]. As shown in Figure 4, when θ = 0.06 deg, the temporal width of sum power is 3.2 fs, and the fluctuation of the homodyne current is small. When the angle increases, as shown in Figure 4b, with θ = 0.16 deg, the temporal width is 4.72 fs, and the homodyne current fluctuates more frequently. Hence, the temporal width with θ = 0.06 deg is rather narrower than the one in the case with θ = 0.16 deg, corresponding to 1.75 and 2.67 cycles of the biphotons, respectively. The smaller θ could help to produce the single cycle biphotons with narrower temporal width (see Fig. 5a) and less cycles. Figure 5b shows the cycles of the biphotons versus the temperature at different angles. It can be found from this figure that the angle is the main factor for the generation of the biphotons, and the cycles of the biphotons becomes gradually larger with the increase of temperature. These characteristics are consistent with the variation of the count rate, the bandwidth of the biphotons with temperature in Figure 3. They are all determined by the phase mismatch function Δk.

thumbnail Fig. 4

Normalized sum power and homodyne current detected by homodyning when temperature T = 25 °C with angles (a) θ = 0.06 deg and (b) θ = 0.16 deg in noncollinear SPDC. And the values shown in the left and right longitudinal axis in each figures are sum powers and homodyne current, respectively.
thumbnail Fig. 5

(a) Normalized sum power with the angle θ = 0.06 deg and θ = 0.16 deg when the temperature T = 25 °C; (b) the cycles of biphotons versus temperature with different angles in noncollinear SPDC.

5 Conclusion

In conclusion, we study on the influence of temperature for generating single cycle biphotons during the noncollinear SPDC in the chirped QPM PPLN crystal. In the numerical simulation of noncollinear SPDC, characteristics of the generated biphotons are deeply determined by the phase mismatching function which is dependent on the angle and the temperature. And the angle plays a more significant role in noncollinear SPDC. Within the appropriate ranges of angle and temperature, the smaller angle and lower temperature could lead the better phase matching effect. Based on such condition, for a certain appropriate angle in noncollinear SPDC, the increase of temperature decreases the count rate of the biphotons and narrows its bandwidth, meanwhile widens the temporal width. However, as long as the angle and temperature are suitable, the biphotons generated by SPDC in the chirped QPM PPLN crystal are ultrashort pulses with single cycles. We hope that our work can find the optimal angle and temperature range for phase matching, so that the generated ultrafast biphotons have a wider spectrum and less cycles. This is of crucial importance in experiments producing ultrafast biphotons entangled through SPDC, particularly in PPLN crystals, where biphoton characteristics can be studied by modifying temperature and controlling pulse temporal width at the single cycle level.

Acknowledgments

J.W. sincerely thanks S.E. Harris for his Mathematica codes.

Funding

This research was funded by supported by the High-level Talent Special Support Program (Tai Talent Leadership [2020] No. 4), Skills Master Studio in Taizhou City of Zhejiang Province (Tai Talent Link [2022] No. 48), Taizhou Vocational College Famous Teachers, Technicians, Principals Studio (TaiZhou Education Vocational College [2023] No. 73), and Scientific Research Project of Zhejiang Provincial Department of Education of China (Grant No. [Y202352591]).

Conflicts of interest

The authors declare no conflicts of interest in regards to this article.

Data availability statement

This article has no associated data generated or analyzed data associated with this article cannot be disclosed due to ethical reason.

Author contribution statement

Writing – Original Draft Preparation, Review & Editing, H. L.; Supervision, J. W.

References

  1. You D, Jones RR, Bucksbaum PH, Dykaar DR, Generation of high-power sub-single-cycle 500-fs electromagnetic pulses, Opt. Lett. 18, 290 (1993). https://doi.org/10.1364/OL.18.000290. [Google Scholar]
  2. Brabec T, Krausz F, Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 72, 545 (2000). https://doi.org/10.1103/RevModPhys.72.545. [CrossRef] [Google Scholar]
  3. Lin Q, Zheng J, Becker W, Subcycle pulsed focused vector beams, Phys. Rev. Lett. 97, 253902 (2006). https://doi.org/10.1103/PhysRevLett.97.253902. [Google Scholar]
  4. Marceau C, Gingras G, Witzel B, Excitation with effective subcycle laser pulses, Phys. Rev. Lett. 111, 203005 (2013). https://doi.org/10.1103/PhysRevLett.111.203005. [Google Scholar]
  5. Hine GA, Doleans M, Intrinsic spatial chirp of subcycle terahertz pulsed beams, Phys. Rev. A. 104, 032229 (2021). https://doi.org/10.1103/PhysRevA.104.032229. [Google Scholar]
  6. Cai X, Zhao J, Wang Z, Lin Q, Ultrafast coherent population transfer in two- and three-level quantum systems using sub-cycle and single-cycle pulses, J. Phys. B: At. Mol. Opt. Phys. 46, 175602 (2013). https://doi.org/10.1088/0953-4075/46/17/175602. [Google Scholar]
  7. Wang ZY, Lin Q, Wang ZY, Single-cycle electromagnetic pulses produced by oscillating electric dipoles, Phys Rev. E. 67, 016503 (2003). https://doi.org/10.1103/PhysRevE.67.016503. [Google Scholar]
  8. Sauge S, Swillo M, A single-crystal source of path/polarization entanglement at non-degenerate wavelengths, Opt. Spectrosc. 108, 165–169 (2010). https://doi.org/10.1134/S0030400X10020037. [Google Scholar]
  9. Zhao CY, Tan WH, Propagation characteristics of biphotons in cold atomic vapor, Chin. Opt. Lett. 12, 102701 (2014). https://opg.optica.org/col/abstract.cfm?URI=col-12-10-102701. [Google Scholar]
  10. Dadoenkova YS, et al., Difference-frequency generation of thz radiation via parametric three-wave interaction in CdTe and ZnTe Crystals, Opt. Spectrosc. 124, 712–719 (2018). https://doi.org/10.1134/S0030400X18050053. [Google Scholar]
  11. Klaiber M, et al., Subcycle time-resolved nondipole dynamics in tunneling ionization, Phys. Rev. A 105, 053107 (2022). https://doi.org/10.1103/PhysRevA.105.053107. [Google Scholar]
  12. Chen Y, Liu CD, Li RX, Probing Rashba spin-orbit coupling by subcycle lightwave control of valley polarization, Phys. Rev. Res. 5, 013098 (2023). https://doi.org/10.1103/PhysRevResearch.5.013098. [Google Scholar]
  13. Iskhakov T, Chekhova MV, Leuchs G, Generation and direct detection of broadband mesoscopic polarization-squeezed vacuum, Phys. Rev. Lett. 102, 183602 (2009). https://doi.org/10.1103/PhysRevLett.102.183602. [CrossRef] [Google Scholar]
  14. Keller TE, Timothy E, Rubin MH, Theory of two-photon entanglement for spontaneous parametric down-conversion driven by a narrow pump pulse, Phys. Rev. A. 56, 1534 (1997). https://doi.org/10.1103/PhysRevA.56.1534. [Google Scholar]
  15. Chekhova MV, et al., Spectral properties of three-photon entangled states generated via three-photon parametric down-conversion in a χ(3) medium, Phys. Rev. A 72, 023818 (2005). https://doi.org/10.1103/PhysRevA.72.023818. [Google Scholar]
  16. Paterova A, et al., Nonlinear infrared spectroscopy free from spectral selection, Sci. Rep. 7, 42608 (2017). https://doi.org/10.1038/srep42608. [Google Scholar]
  17. Lindner C, et al., Fourier transform infrared spectroscopy with visible light, Opt. Express 28(4), 4426 (2020). https://doi.org/10.1364/OE.382351. [Google Scholar]
  18. Hojo M, Tanaka K, Broadband infrared light source by simultaneous parametric down-conversion, Sci. Rep. 11, 17986 (2021). https://doi.org/10.1038/s41598-021-97531-w. [Google Scholar]
  19. Dauler E, Jaeger G, Muller A, Migdall A, Sergienko A, Tests of a two-photon technique for measuring polarization mode dispersion with subfemtosecond precision, J. Res. Natl. Inst. Stand. Techn. 104, 1 (1999). https://doi.org/10.6028/jres.104.001. [Google Scholar]
  20. Fraine A, Minaeva O, Simon DS, Egorov E, Sergienko AV, Broadband source of polarization entangled photons, Opt. Lett 37, 1910 (2012). https://doi.org/10.1364/OL.37.001910. [Google Scholar]
  21. Gatti A, Corti T, Brambilla E, Horoshko DB, Dimensionality of the spatiotemporal entanglement of parametric down-conversion photon pairs, Phys. Rev. A. 86, 053803 (2012). https://doi.org/10.1103/PhysRevA.86.053803. [Google Scholar]
  22. Hendrych M, Shi XJ, Valencia A, Torres JP, Broadening the bandwidth of entangled photons: A step towards the generation of extremely short biphotons, Phys. Rev. A. 79, 023817 (2009). https://doi.org/10.1103/PhysRevA.79.023817. [Google Scholar]
  23. Harris SE, Chirp and compress: toward single-cycle biphotons, Phys. Rev. Lett. 98, 063602 (2007). https://doi.org/10.1103/PhysRevLett.98.063602. [NASA ADS] [CrossRef] [Google Scholar]
  24. Pignatiello F, et al., Measurement of the thermal expansion coefficients of ferroelectric crystals by a moiré interferometer. Opt. Comm. 277, 1 2007. https://doi.org/10.1016/j.optcom.2007.04.045. [Google Scholar]
  25. Tanaka A, et al., Noncollinear parametric fluorescence by chirped quasi-phase matching for monocycle temporal entanglement, Opt. Exp. 20, 25228 (2012). https://doi.org/10.1364/OE.20.025228. [Google Scholar]
  26. Fejer MM, et al., Quasi-phase-matched second harmonic generation: tuning and tolerances. IEEE J. Quant. Electron. 28(11), 2631 (1992). https://doi.org/10.1109/3.161322. [Google Scholar]
  27. Tang CL, Cheng LK, Fundamentals of optical parametric processes and oscillators (Harwood Academic Publishers, Amsterdam, 1995). [Google Scholar]
  28. Armstrong JA, et al., Interactions between light waves in a nonlinear dielectric, Phys. Rev. 127, 1918 (1962). https://doi.org/10.1103/PhysRev.127.1918. [CrossRef] [Google Scholar]
  29. Myers LE, et al., Quasi-phase-matched optical parametric oscillators in bulk periodically poled LiNbO3, J. Opt. Soc. Am. B 12, 2102 (1995). https://doi.org/10.1364/JOSAB.12.002102. [CrossRef] [Google Scholar]
  30. Charbonneau-Lefort M, Afeyan B, Fejer MM, Optical parametric amplifiers using chirped quasi-phase-matching gratings I: practical design formulas, J. Opt. Soc. Am. B 25, 463 (2008). https://doi.org/10.1364/JOSAB.25.000463. [NASA ADS] [CrossRef] [Google Scholar]
  31. Wang J, Lin H, The single-cycle biphotons generated by noncollinear SPDC in the chirped QPM crystals, J. Eur. Opt. Society-Rapid Publ. 20, 6 (2024). https://doi.org/10.1051/jeos/2024004. [Google Scholar]
  32. Li BH, Xu YG, Zhu HF, Lin FK, Li YF, Temporal compression and shaping of chirped biphotons using Fresnel-inspired binary phase shaping, Phys. Rev. A 91, 023827 (2015). https://doi.org/10.1103/PhysRevA.91.023827. [Google Scholar]
  33. Nasr MB, et al., Ultrabroadband biphotons generated via chirped quasi-phase-matched optical parametric down-conversion, Phys. Rev. Lett. 100, 183601 (2008). https://doi.org/10.1103/PhysRevLett.100.183601. [NASA ADS] [CrossRef] [Google Scholar]
  34. Pe’er A, Dayan B, Friesem AA, Silberberg Y, Temporal shaping of entangled photons, Phys. Rev. Lett. 94, 073601 (2005). https://doi.org/10.1103/PhysRevLett.94.073601. [Google Scholar]
  35. Hobden MV, Warner J, The temperature dependence of the refractive indices of pure lithium niobate, Phys. Lett. 22, 243 (1966). https://doi.org/10.1016/0031-9163(66)90591-9. [Google Scholar]
  36. Edwards GJ, Lawrence M, A temperature-dependent dispersion equation for congruently grown lithium niobate, Opt. Quantum Electron. 16, 373 (1984). https://doi.org/10.1007/BF00620081. [Google Scholar]
  37. Jundt DH, Temperature-dependent Sellmeier equation for the index of refraction, ne, in congruent lithium niobate, Opt. Lett 20 (22), 1553 (1997). https://doi.org/10.1364/OL.22.001553. [Google Scholar]
  38. Deng LH, et al., Improvement to Sellmeier equation for periodically poled LiNbO3 crystal using mid-infrared difference-frequency generation, Opt. Comm. 268, 110 (2006). https://doi.org/10.1016/j.optcom.2006.06.082. [Google Scholar]

All Figures

thumbnail Fig. 1

Scheme of noncollinear SPDC in chirped QPM PPLN crystal. The directions of arrows in the crystal represent polarized axis for the QPM PPLN crystal. The pump, signal and idler lights are denoted by p, s, i respectively.
In the text
thumbnail Fig. 2

The ∆k/ζL versus temperature and frequency with (a) θ = 0.06 deg; (b) θ = 0.16 deg.
In the text
thumbnail Fig. 3

(a) The count rate and (b) the bandwidth of biphotons versus the temperature for different angles θ.
In the text
thumbnail Fig. 4

Normalized sum power and homodyne current detected by homodyning when temperature T = 25 °C with angles (a) θ = 0.06 deg and (b) θ = 0.16 deg in noncollinear SPDC. And the values shown in the left and right longitudinal axis in each figures are sum powers and homodyne current, respectively.
In the text
thumbnail Fig. 5

(a) Normalized sum power with the angle θ = 0.06 deg and θ = 0.16 deg when the temperature T = 25 °C; (b) the cycles of biphotons versus temperature with different angles in noncollinear SPDC.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.