| Issue |
J. Eur. Opt. Society-Rapid Publ.
Volume 19, Number 1, 2023
EOSAM 2022
|
|
|---|---|---|
| Article Number | 32 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/jeos/2023029 | |
| Published online | 08 June 2023 | |
Short Communication
Experimental and numerical polarization analysis of the 3D transfer behavior in microsphere-assisted interferometry for 1D phase gratings
Measurement Technology Group, Faculty of Electrical Engineering and Computer Science, University of Kassel, Wilhelmshöher Allee 71, 34121 Kassel, Germany
* Corresponding author: lucie.hueser@uni-kassel.de
Received:
27
January
2023
Accepted:
2
May
2023
Enhancing the lateral resolution in optical microscopy and interferometry is of great interest in recent research. In order to laterally resolve structures including feature dimensions below the Abbe resolution limit, microspheres in the optical near-field of the specimen are shown to locally improve the resolution of the imaging system. Experimental and simulated results following this approach are obtained by a high NA Linnik interferometer and analyzed in this contribution. They show the reconstructed surface of a 1D phase grating below the resolution limit. For further understanding of the transfer characteristics, measured interference data are compared with FEM (finite element method) based simulations with respect to the polarization dependency of the relevant image information for 1D phase gratings. Therefore, the implemented Koehler illumination as well as the experimental setup utilize polarized light.
Key words: Interferometry / Microsphere / Resolution / CSI / Polarization
© The Author(s), published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
With the ongoing trend towards miniaturization overcoming Abbe’s diffraction limit in optical metrology is of particular interest regarding research and industrial applications. Microsphere assistance is known as a technique to achieve topographical interferometric [1–3] as well as microscopic [4, 5] measurements of structures below the resolution limit through near-field support. Photonic nanojets are frequently mentioned as the most decisive mechanism [6–8] in this context. Also the role of evanescent waves and whispering gallery modes [9, 10] is discussed. It is also found that the polarization of the illuminating light has an influence on the resolution capabilities when using microspheres [5]. More recently, a combination of the small field of view with the effectively enhanced numerical aperture of the system is found to be the most likely underlying physical mechanism [11, 12].
In optical imaging microscopy the fundamental resolution limit for periodic structures is according to Ernst Abbe given by,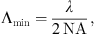 (1)where Λmin is the minimal period length of a structure that can be resolved, NA is the numerical aperture of the system and λ is the central illumination wavelength. Placing microspheres directly on the measurement object enables to reconstruct surfaces with periodic features below this limit. Several publications show also attempts to include microspheres in more practicable positioning systems, e.g. the attachment of microspheres on cantilevers or trapping them with optical tweezers [12].
(1)where Λmin is the minimal period length of a structure that can be resolved, NA is the numerical aperture of the system and λ is the central illumination wavelength. Placing microspheres directly on the measurement object enables to reconstruct surfaces with periodic features below this limit. Several publications show also attempts to include microspheres in more practicable positioning systems, e.g. the attachment of microspheres on cantilevers or trapping them with optical tweezers [12].
In this contribution the effects of illumination polarization are examined with respect to interference microscopy. Thus, measured as well as rigorously simulated data sets of a grating with periodicity close to the resolution limit are compared with respect to polarization. Throughout this paper for TM polarization the electric field component is defined in the same plane as the 1D phase grating (x, z) similar to [13]. The results are analyzed in the 3D spatial frequency domain in order to find out the transfer characteristics and compare them for simulation and measurement results. Furthermore, a grating with period below the resolution limit was measured and the result of the interference phase analysis is shown.
2 Experimental setup and measurement results
Experimental results are obtained using a high NA Linnik interferometer (100×, NA = 0.9). The measurement process follows the principle of coherence scanning interferometry (CSI) and is described in further detail in [1]. For image acquisition a depth scan with a step size of 20 nm is performed by the piezo scanner. The resulting image stack is analyzed with respect phase and envelope of the interference signals resulting in a reconstructed surface topography of the measured specimen. Koehler illumination with an LED (royalblue, central wavelength: approximately λ = 440 nm) is used in order to provide spatially incoherent illumination. This leads to a resolution limit of Λmin = 244 nm. A schematic representation of the experimental setup is shown in Figure 1.
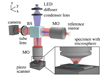 |
Fig. 1 Schematic representation of the microsphere assisted Linnik interferometer comprising two high NA microscope objective lenses (MO) and a beam splitter (BS). The illumination (blue, representing Koehler illumination) and imaging (red) beam paths are shown. The illumination beam path appearing as a plane wave below the objective lens is omitted for better visibility. The figure is not drawn to scale to enhance the comprehensibility. |
When using microsphere enhancement, grating periods of 230 nm length were successfully measured. A result of a reconstructed surface topography is shown in Figure 2. In this result the magnification factor of 1.4 induced by the microsphere can be observed [11]. A phase evaluation algorithm based on a lock-in algorithm further elaborated in [14] is used to analyze the acquired interference signals. The measured specimen was a linewidth/pitch standard fabricated by supracon.
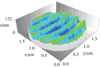 |
Fig. 2 Measurement result of a 230 nm grating (linewidth/pitch standard). For phase analysis of the interference signals an evaluation wavelength of 650 nm was used. The dependency of the evaluation wavelength on the phase evaluation algorithm used for the surface reconstruction is elaborated in [1]. |
3 Rigorous simulation of the imaging process
Several attempts have been discussed in recent publications on theoretical and simulation studies of microsphere-assisted interferometry and microscopy. One of the most common approaches, which is also directly related to the analysis of photonic nanojets, is a rigorous simulation of a microsphere in free space illuminated by a plane wave source [7]. While this illustrates in detail the formation of nanojets, several aspects relevant to the overall imaging process in a microscope-based measurement setup are neglected [15].
Pahl et al. [13] developed a rigorous CSI simulation model based on FEM calculation of the electric field distribution near the sample and Fourier optics modeling of the imaging process. This model accounts for 3D conical illumination in a microscope and has recently been extended to include a microcylinder to approximate microsphere-assisted interferometry [16]. It represents a rigorous approach to the theoretical representation of interferometric imaging processes. Conical illumination is implemented with a discretization of angles of incidence homogeneously filling the numerical aperture of the system. This approach enables to consider Koehler illumination. Using the calculated near-field data sets, a far-field expansion is performed for each angle of incidence separately, leading to a Fourier optical representation of the imaging system considering the reference plane. The resulting intensity distributions are incoherently superimposed, resulting in [13]: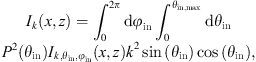 (2)with φin representing the conical incident angle and θin,max = arcsin(NA) the maximum opening angle of the aperture. With P(θin) the pupil function for both, the reference and the object arm is considered. The intensity
(2)with φin representing the conical incident angle and θin,max = arcsin(NA) the maximum opening angle of the aperture. With P(θin) the pupil function for both, the reference and the object arm is considered. The intensity  is the intensity distribution for each angle φin and θin,max calculated from the simulated electric field distributions. Taking the spectral distribution S(k) of the light source with the wave number k = 2π/λ into account the total intensity
is the intensity distribution for each angle φin and θin,max calculated from the simulated electric field distributions. Taking the spectral distribution S(k) of the light source with the wave number k = 2π/λ into account the total intensity 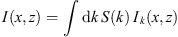 is calculated.
is calculated.
Finally, signal processing algorithms (e.g. phase and envelope evaluation algorithms) are applied to the a stack of simulated interference images. This corresponds to the signal processing performed on experimentally obtained image stacks, thus providing direct comparability.
4 Analysis of the results in the 3D spatial frequency domain
The transfer characteristics of an interferometer can be obtained from the 3D spatial frequency domain representation of a measured data set [17], which enables a profound understanding of the 3D measurement process. This method is applied to microsphere-assisted interferometry to gain further insight into the mechanisms underlying the lateral resolution enhancement.
For further analysis the data is transferred to the 3D spatial frequency domain also called q–space, which is based on the incident wave vectors kin and the scattered wave vectors ks defined as, and therefore q = ks − kin holds.
and therefore q = ks − kin holds.
The resulting 3D spatial frequency distribution is limited by the Ewald limiting sphere, which is shown in Figure 3 and explained in further detail in [17]. Thus, the diffraction orders qx,n = 2πn/Λ with n ∈ {…, −1, 0, 1,…} for a grating of period length Λ in x-direction appear as distinct vertical lines within the Ewald limiting sphere, as exemplarily shown in Figure 3.
 |
Fig. 3 Representation of the Ewald limiting sphere for monochromatic light of wave number k0 in q – space. The q – values belonging to specular reflection (qx = 0) and backscattering are marked. The most outlying edges at qx = ±2k0NA correspond to the highest resolvable spatial frequencies for the maximum incident angle θin,max. kr is representing the reflected wave vector. As an example, the first diffraction orders for a periodic structure with a period length Λ were inserted. |
To illustrate the connection between the q–space representation of the interferometric measurement data stack 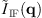 and the 3D transfer function HIF(q) the following equation can be used for the interference part of the signal [17]:
and the 3D transfer function HIF(q) the following equation can be used for the interference part of the signal [17]:![$$ {^\tilde{I}}_{\mathrm{IF}}(\mathbf{q})=[{^\tilde{U}}_0\left(\mathbf{q}\right)\otimes {^\tilde{U}}_{\mathrm{ref}}\left(\mathbf{q}\right){]}_{{q}_x,{q}_y}H\left(\mathbf{q}\right), $$](/articles/jeos/full_html/2023/01/jeos20230005/jeos20230005-eq7.gif) (3)
(3)
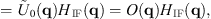 (4)where
(4)where 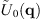 denotes the scattered light field of the phase object in q–space. Since the reference plane is a mirror, all contributions to the signal formation lie on the qz-axis, and the contribution of
denotes the scattered light field of the phase object in q–space. Since the reference plane is a mirror, all contributions to the signal formation lie on the qz-axis, and the contribution of 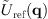 to the correlation (denoted with ⊗) can be considered by HIF(q). O(q) represents the 3D object spectrum if the surface is represented by a thin foil [18]. Using the inverse Fourier transform, the interference measurement data stack in the spatial domain is given by the convolution of the surface foil o(x, y, z) and the real part hIF(x, y, z) of the inverse Fourier transformed function HIF(q), therefore (with * denoting the convolution),
to the correlation (denoted with ⊗) can be considered by HIF(q). O(q) represents the 3D object spectrum if the surface is represented by a thin foil [18]. Using the inverse Fourier transform, the interference measurement data stack in the spatial domain is given by the convolution of the surface foil o(x, y, z) and the real part hIF(x, y, z) of the inverse Fourier transformed function HIF(q), therefore (with * denoting the convolution), (5)
(5)
This shows that by analyzing the transfer behavior of the system including the microspheres, which strongly affect the imaging capabilities, important insight into relevant mechanisms can be gained.
Figures 4a–4d show measured and simulated interferometric data sets for a rectangular silicon grating (RS-N, SiMETRICS) with Λ = 300 nm and a nominal height of 140 nm. The phase grating leads to a phase modulation of the interference fringes along the x-axis, which is centered around the virtual image plane of the microsphere [1].
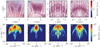 |
Fig. 4 Interferometric measurement data obtained from a rectangular grating (SiMETRICS RS-N, Λ = 300 nm) using royalblue (a) TM and (b) TE polarized light through a microsphere (SiO2, 5–9 μm diam.), simulated data sets of a similar grating with (c) TM and (d) TE polarized light assuming a microcylinder of 5 μm diameter. The corresponding 3D spatial frequency representations are depicted in (e) – (h). The results shown in (a) and (e) are also analyzed in [11]. |
Comparing the different polarization configurations it can be observed that for TM polarized light the phase modulation induced by the grating is much stronger in both, measurement and simulation results. Besides, a qualitative correspondence of measured and simulated results can be seen. Therefore, the simulation approach in principle reproduces the transfer characteristics of microsphere-assisted interferometry.
In Figures 4e–4h the 3D spatial frequency domain representations in the qx qz-plane of the different data sets are depicted. The first order diffracted light components appear at qx ≈ ±15 μm−1 (considering the additional magnification through the microsphere). Instead of distinct vertical lines the diffraction maxima are blurred. This effect can be explained by the limited field of view while imaging through a microsphere. In Fourier optics the field of view corresponds to the area of integration for the Fourier integral, which can be considered by multiplication with an appropriate function describing the limited extension of the illuminated area in the object space under the microsphere. This leads to a convolution with the Fourier transformed illumination function in the Fourier domain and thus explains the broadening of the diffraction orders.
Comparing the frequency representations for the TM and TE case, the intensity maxima related to first order diffraction are lower for the TE case, which is in agreement with the weaker phase modulation visible in Figure 4b. In comparison with the simulated results in the 3D spatial frequency domain, some effects occur differently. The magnification introduced by the microcylinder is higher (compare the extension in x-direction of the phase modulation in Figs. 4a and 4c), leading to slightly different positions of the diffraction orders. Furthermore, due to the use of a 2D microcylinder instead of a sphere in the simulation further effects appear [11]. Also slight differences in the diameter of the utilized microspheres compared to the microcylinder affect the results.
For a better differentiation of the results shown in Figure 4 of simulated interferometric data sets without microspheres are shown in Figure 5. For the TM polarization in Figure 5a, a stronger modulation of the phase laterally can be seen here. This corresponds to the results recorded with microsphere assistance.
 |
Fig. 5 Simulated interferometric data set with a rectangular grating structure similar to the SiMETRICS RS-N grating as a specimen (Λ = 300 nm) for the (a) TM and (b) TE polarization case. |
5 Conclusion
Considering the transfer behavior of an optical system enhanced with microspheres placed in the near-field of a specimen, gives insight into the relevant mechanisms. Here, the influence of the polarization of the illuminating light is examined. It is pointed out how the transfer behavior of the optical imaging process including the microsphere contributes to a deeper understanding of the relevant mechanisms for imaging capabilities and resolution enhancement.
Analyzing the polarization dependency, TM polarization should be preferred to obtain the relevant phase information of 2D topographies, which are shift-invariant in y-direction. This is in agreement with previous results obtained for grating structures using an interference microscope without microsphere assistance and could be confirmed by rigorous simulations based on an FEM model [13].
Further, the reconstructed topography of a grating structure with a period length below Abbe’s resolution limit is shown to demonstrate the improved resolution enabled by the microsphere introduced into the optical system.
Conflict of interest
The authors declare that they have no conflicts of interest in relation to this article.
Acknowledgments
The partial support of this project by the DFG (German Research Foundation) under grant number LE992/15-1 is gratefully acknowledged.
References
- Hüser L., Lehmann P. (2020) Microsphere-assisted interferometry with high numerical apertures for 3D topography measurements, Appl. Opt. 59, 1695. [CrossRef] [Google Scholar]
- Perrin S., Donie Y.J., Montgomery P., Gomard G., Lecler S. (2020) Compensated microsphere-assisted interference microscopy, Phys. Rev. Appl. 13, 1. [CrossRef] [Google Scholar]
- Wang F., Liu L., Yu P., Liu Z., Yu H., Wang Y., Li W.J. (2016) Three-dimensional super-resolution morphology by near-field assisted white-light interferometry, Sci. Rep. 6, 24703. [NASA ADS] [CrossRef] [Google Scholar]
- Wang Z., Guo W., Li L., Luk’yanchuk B., Khan A., Liu Z., Chen Z., Hong M. (2011) Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope, Nat. Commun. 2, 218. [NASA ADS] [CrossRef] [Google Scholar]
- Darafsheh A., Walsh G.F., Dal Negro L., Astratov V.N. (2012) Optical super-resolution by high-index liquid-immersed microspheres, Appl. Phys. Lett. 101, 141128. [NASA ADS] [CrossRef] [Google Scholar]
- Yang H., Trouillon R., Huszka G., Gijs M.A. (2016) Super-resolution imaging of a dielectric microsphere is governed by the waist of its photonic nanojet, Nano Lett. 16, 4862. [NASA ADS] [CrossRef] [Google Scholar]
- Darafsheh A. (2021) Photonic nanojets and their applications, J. Phys.: Photon. 3, 022001. [NASA ADS] [CrossRef] [Google Scholar]
- Lecler S., Perrin S., Leong-Hoi A., Montgomery P. (2019) Photonic jet lens, Sci. Rep. 9, 1. [Google Scholar]
- Ben-Aryeh Y. (2016) Increase of resolution by use of microspheres related to complex Snell’s law, J. Opt. Soc. Am. A 33, 2284. [NASA ADS] [CrossRef] [Google Scholar]
- Zhou S., Deng Y., Zhou W., Yu M., Urbach H.P., Wu Y. (2017) Effects of whispering gallery mode in microsphere super-resolution imaging, Appl. Phys. B: Lasers Opt. 123, 1. [NASA ADS] [CrossRef] [Google Scholar]
- Hüser L., Pahl T., Künne M., Lehmann P. (2022) Microsphere assistance in interference microscopy with high numerical aperture objective lenses, J. Opt. Microsyst. 2, 044501. [Google Scholar]
- Darafsheh A. (2022) Microsphere-assisted microscopy, J. Appl. Phys. 131, 031102. [NASA ADS] [CrossRef] [Google Scholar]
- Pahl T., Hagemeier S., Künne M., Yang D., Lehmann P. (2020) 3D modeling of coherence scanning interferometry on 2D surfaces using FEM, Opt. Express 28, 39807. [CrossRef] [Google Scholar]
- Lehmann P., Tereschenko S., Xie W. (2016) Fundamental aspects of resolution and precision in vertical scanning white-light interferometry, Surf. Topogr.: Metrol. Prop. 4, 024004. [NASA ADS] [CrossRef] [Google Scholar]
- Wang Z., Luk’yanchuk B. (2019) Super-resolution imaging and microscopy by dielectric particle-lenses, Springer International Publishing, Cham, pp. 371–406. ISBN 978-3-030-21722-8. [Google Scholar]
- Pahl T., Hüser L., Hagemeier S., Lehmann P. (2022) FEM-based modeling of microsphere-enhanced interferometry, Light: Adv. Manuf. 3, 1. [Google Scholar]
- Lehmann P., Künne M., Pahl T. (2021) Analysis of interference microscopy in the spatial frequency domain, J. Phys.: Photon. 3, 1. [Google Scholar]
- Coupland J., Mandal R., Palodhi K., Leach R. (2013) Coherence scanning interferometry: Linear theory of surface measurement, Appl. Opt. 52, 3662. [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic representation of the microsphere assisted Linnik interferometer comprising two high NA microscope objective lenses (MO) and a beam splitter (BS). The illumination (blue, representing Koehler illumination) and imaging (red) beam paths are shown. The illumination beam path appearing as a plane wave below the objective lens is omitted for better visibility. The figure is not drawn to scale to enhance the comprehensibility. |
| In the text | |
 |
Fig. 2 Measurement result of a 230 nm grating (linewidth/pitch standard). For phase analysis of the interference signals an evaluation wavelength of 650 nm was used. The dependency of the evaluation wavelength on the phase evaluation algorithm used for the surface reconstruction is elaborated in [1]. |
| In the text | |
 |
Fig. 3 Representation of the Ewald limiting sphere for monochromatic light of wave number k0 in q – space. The q – values belonging to specular reflection (qx = 0) and backscattering are marked. The most outlying edges at qx = ±2k0NA correspond to the highest resolvable spatial frequencies for the maximum incident angle θin,max. kr is representing the reflected wave vector. As an example, the first diffraction orders for a periodic structure with a period length Λ were inserted. |
| In the text | |
 |
Fig. 4 Interferometric measurement data obtained from a rectangular grating (SiMETRICS RS-N, Λ = 300 nm) using royalblue (a) TM and (b) TE polarized light through a microsphere (SiO2, 5–9 μm diam.), simulated data sets of a similar grating with (c) TM and (d) TE polarized light assuming a microcylinder of 5 μm diameter. The corresponding 3D spatial frequency representations are depicted in (e) – (h). The results shown in (a) and (e) are also analyzed in [11]. |
| In the text | |
 |
Fig. 5 Simulated interferometric data set with a rectangular grating structure similar to the SiMETRICS RS-N grating as a specimen (Λ = 300 nm) for the (a) TM and (b) TE polarization case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


