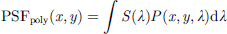| Issue |
J. Eur. Opt. Society-Rapid Publ.
Volume 19, Number 1, 2023
|
|
|---|---|---|
| Article Number | 22 | |
| Number of page(s) | 17 | |
| DOI | https://doi.org/10.1051/jeos/2023013 | |
| Published online | 28 April 2023 | |
Research Article
Method for assessing the impact of residual roughness after corneal ablation simulated as random and filtered noise in polychromatic vision
1
Research and Development, SCHWIND Eye-Tech-Solutions, 63801 Kleinostheim, Germany
2
Interdisciplinary Center for Scientific Computing (IWR), Universität Heidelberg, 69117 Heidelberg, Germany
3
Mannheim Institute for Intelligent Systems in Medicine (MIISM), Universität Heidelberg, 69117 Heidelberg, Germany
4
Central Institute for Computer Engineering (ZITI), Universität Heidelberg, 69117 Heidelberg, Germany
5
CZS Heidelberg Center for Model-Based AI, Universität Heidelberg, 69117 Heidelberg, Germany
* Corresponding author: shwetabh.verma@yahoo.com
Received:
17
November
2022
Accepted:
20
March
2023
Purpose: Despite theoretical models for achieving laser-based ablation smoothness, methods do not yet exist for assessing the impact of residual roughness after corneal ablation, on retinal polychromatic vision. We developed a method and performed an exploratory study to qualitatively and quantitatively analyze the impact of varying degree of corneal roughness simulated through white and filtered noise, on the retinal image. Methods: A preliminary version of the Indiana Retinal Image Simulator (IRIS) [Jaskulski M., Thibos L., Bradley A., Kollbaum P., et al. (2019) IRIS – Indiana Retinal Image Simulator. https://blogs.iu.edu/corl/iris] was used to simulate the polychromatic retinal image. Using patient-specific Zernike coefficients and pupil diameter, the impact of different levels of chromatic aberrations was calculated. Corneal roughness was modeled via both random and filtered noise [(2013) Biomed. Opt. Express 4, 220–229], using distinct pre-calculated higher order Zernike coefficient terms. The outcome measures for the simulation were simulated retinal image, Strehl Ratio and Visual Strehl Ratio computed in frequency domain (VSOTF). The impact of varying degree of roughness (with and without refractive error), spatial frequency of the roughness, and pupil dilation was analyzed on these outcome measures. Standard simulation settings were pupil size = 6 mm, Defocus Z[2, 0] = 2 μm (−1.54D), and Spherical Aberrations Z[4, 0] = 0.15 μm. The signal included the 2–4th Zernike orders, while noise used 7–8th Zernike orders. Noise was scaled to predetermined RMS values. All the terms in 5th and 6th Zernike order were set to 0, to avoid overlapping of signal and noise. Results: In case of a constant roughness term, reducing the pupil size resulted in improved outcome measures and simulated retinal image (Strehl = 0.005 for pupil size = 6 mm to Strehl = 0.06 for pupil size = 3 mm). The calculated image quality metrics deteriorated dramatically with increasing roughness (Strehl = 0. 3 for no noise; Strehl = 0.03 for random noise of 0.25 μm at 6 mm diameter; Strehl = 0.005 for random noise of 0.65 μm at 6 mm diameter). Clear distinction was observed in outcome measures for corneal roughness simulated as random noise compared to filtered noise, further influenced by the spatial frequency of filtered noise. Conclusion: The proposed method enables quantifying the impact of residual roughness in corneal ablation processes at relatively low cost. Since normally laser ablation is an integral process divided on a defined grid, the impact of spatially characterized noise represents a more realistic simulation condition. This method can help comparing different refractive laser platforms in terms of their associated roughness in ablation, indirectly improving the quality of results after Laser vision correction surgery.
Key words: Residual roughness / Cornea ablation / Random and filtered noise / Polychromatic vision / Ablation smoothness
© The Author(s), published by EDP Sciences, 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The human eye is a sophisticated optical system where the state of visual optics defines many important aspects of visual performance, such as acuity and contrast sensitivity. The retinal image formed by the eye is the basis of the human vision, which is later perceived by the brain to complete the vision process. In order to qualitatively and quantitatively analyze the performance of the eye, retinal image produced by an arbitrary acuity target can be calculated. Starting from this calculated retinal image, authors have proposed models of the complete acuity task, including optical filtering of the optotype targets, some form of neural processing, noise, and a final template matching operation to identify the target [1, 2]. The optical performance of any optical system including human eye is often described in terms of the wavefront error at the exit pupil. Standardized methods have been developed to describe these errors over the pupil size, as a sum of a set of weighted Zernike polynomials [3]. These wavefront errors can be used to compute the optical visual point spread function (PSF), and to thereby calculate the retinal image [4].
Attempts have also been made to develop optical quality metrics for the human eye that correlate well with visual performance. Although some of these metrics have proven quite successful at predicting visual acuity [5–7], refractive error [8], or subjective blur [9], they have been based upon monochromatic descriptions of the eye’s optical quality. Human vision generally involves polychromatic stimuli, which suggests the need for polychromatic measures of retinal image quality; however, the wavefront error of the eye is typically diagnosed with monochromatic stimuli. The complex interactions between monochromatic and chromatic aberrations in forming the retinal image [10, 11] has provided motivation to develop computational methods for characterizing the optical quality of the eye that incorporate both types of aberrations. Few general approaches have been proposed in the past for computing the polychromatic image quality of the human eye from a single measure of monochromatic aberrations [12–14].
Quantification of expected benefit and visual performance is based on different metrics generally grouped under the name of Visual Strehl (VS) related with wavefront error, optical transfer function, point spread function and correlation with templates. The variety of different criteria bear witness to the difficulty of the task. Visual Strehl Ratio can be calculated in the frequency domain, based on a scaled Modulation Transfer Function or on the real part of the scaled optical transfer function. Visual Strehl Ration scaled by the neural Contrast Sensitivity Function has been claimed to be the best descriptor of visual performance that can be calculated from wavefront aberrations data. Although VSOTF has been considered as a benchmark metric to quantify the modelled image quality [5], several authors point out that this criterion is better suited to symmetrical aberrations as opposed their high order counterpart. In fact, it is considered that when working with non-symmetrical aberrations it is better to use metrics that emphasize the relevance of the Optical Transfer Function (Phase Transfer Function or the PTF), especially when searching for correlations with letter identification and predicting visual acuity [15, 16].
Arines et al. [15] compared VSOTF and the criterion suggested by Young et al. [17] called Visual Strehl Combined (VSCombined) with numerical simulations and experimental data. They found that the VSOTF predicted the non-visibility of the letters presenting very small values (also observed in our simulations), similar to those of 2D out of focus images, although they were readable. In contrast, the VSCombined showed better correlation with the visual experience of the letters. While VSOTF provides information about the effect of contrast reduction due to aberrations, VSCombined weighs the effect of phase reversal and PTF modulation on final image quality. It is difficult to establish a clear criterion to assess the performance of extended depth of field solutions. VSOTF provides information mainly about the contrast transfer of the evaluated element while VSCombined provides information on the amount of phase difference between the different frequencies transmitted by the system [15]. It is important to quantify not only contrast loss but also PTF when evaluating non-symmetrical phase elements. A Combination of VSOTF and VSCombined would enable evaluation of contrast transfer and changes in PTF, however such a combination image quality metric was not evaluated in our simulations.
Precise lasers with small laser spots and high repetition rates are now widely used to manipulate the shape of the cornea to correct refractive errors. Corneal remodeling is essentially similar to any other form of micro-machining. The lasers used in micro-machining are normally pulsed excimer lasers, where the duration of the pulses is very short compared to the time period between the pulses. Despite attempts for achieving high levels of ablation smoothness [18–21] laser corneal refractive surgery still presents some challenges in terms of the residual roughness associated with the cornea postoperatively (Fig. 1 [20]). This residual roughness may influence the epithelium to respond in a way that produces haze, regression and reduced accuracy of refractive correction, to degrade overall visual performance [22]. Figure 1 shows an oversimplified sketch of how roughness is induced during the pulse-by-pulse ablation process. In the first frame, a set of laser pulses target the ablation volume. The residual roughness from the first set of laser pulses is targeted in the second frame. Finally, in the third frame, the residual roughness remains that is a combination of the residual roughness of the previous frames, limited by the maximum ablation depth at each location. In this manner, the residual roughness depends on several factors like the laser beam characteristics (like spot energy, spot diameter, super Gaussian order, truncation radius, spot geometry), spot overlap and the lattice geometry used in ablation [20].
 |
Fig. 1 Schematic representation of how the roughness is induced during the pulse-by-pulse ablation process – exaggerated scale. The letters correspond to arbitrary areas (in yellow) in which the residual ablation is evaluated, whereas numbers represent individual laser pulses. The thick horizontal line represents the target ideal surface (without any roughness). |
Vinciguerra et al. used a Nidek Eas-1000 Anterior Eye Segment Analysis System to examine the ablated surface or the interface regularity immediately after photorefractive keratectomy (PRK) and laser in situ keratomileusis (LASIK) [23]. At 12 months postoperatively, they found that patients with no postoperative irregularity had a sharply lower incidence of haze and a better refractive outcome compared to patients showing corneal irregularity. Comparatively LASIK has shown better short-term visual acuities than PRK due to the differences in healing of the epithelium [24]. Although improvement in uncorrected visual acuity is more rapid in LASIK, efficacy outcomes in the longer term generally are similar between the two procedures [25, 26]. On the other hand, epithelial remodeling (change with respect to preoperative status) occurs strongly in LASIK compared to surface ablations, resulting in the outcomes being affected more strongly due to residual roughness in the mid-term and long term [27]. Performing a final smoothing immediately after PRK or LASIK has been advocated to further improve refractive and optical outcomes [28]. The claims that surface ablation induces roughness needs to be conditioned with the clinical impact on vision since measuring vision is the endpoint. Furthermore, the induced roughness is generally ameliorated by epithelial resurfacing leaving an optically acceptable interface, aiding the postoperative vision.
Although theoretical models and software exist to qualitatively and quantitatively compute the monochromatic and polychromatic retinal image for given state of the eye optics, to the best of our knowledge, there are no proposed methods applying these models to analyze the impact of residual roughness associated with laser ablation of the cornea in refractive surgery. As solution, this work proposes a method to convert wavefront aberrations modified for a varying degree of roughness, characteristic to the laser ablation process, to a visual PSF, in order to calculate the polychromatic retinal image. Using this approach, the aim of this study is to analyze the impact of varying degree of corneal roughness (characterized as random and filtered noise), on the retinal image, qualitatively and quantitatively.
2 Methods
The methods published by Ravikumar et al. [14] were used in the simulations. They employed a model of ocular chromatic aberration based on population average levels of Longitudinal Chromatic Aberrations (LCA), which has been shown to vary little from eye to eye [29], to examine the impact of different levels of monochromatic aberrations and Transverse Chromatic Aberrations (TCA), which are known to vary widely from eye to eye. Based on the methods, polychromatic PSFs were used to compute retinal images for spectrally homogeneous targets.
2.1 Theoretical Background for simulating retinal images
-
The wavefront aberration function of the eye was used to calculate the Monochromatic complex pupil function:
-
where, x and y are the pupil coordinates, P(x, y) is the amplitude component which defines shape, size and transmission of the system pupil, W(x, y) is the wave aberration function, and λ is the reference monochromatic wavelength of light at which the wavefront was defined. The parameter P(x, y) takes the Stiles-Crawford Effect in to account. The wavefront W(x, y) can be defined using a series of Zernike coefficients calculated over a pupil diameter.
-
Monochromatic PSF was calculated from the complex pupil function using Fraunhofer approximation formula:
-
If wavefront aberration maps are available for a representative selection of wavelengths in the spectrum of the polychromatic source, then the calculation of PSF can be repeated at each wavelength to obtain a family of spread functions.
-
In our simulations, we entered the wavefront for a wavelength of 550 nm, and the software estimated the wavefront (high and low order aberrations) for other wavelengths as previously described [30].
-
Polychromatic PSF was calculated using series of such monochromatic PSF and weighting them by the luminance (S(λ)) of the polychromatic source at that wavelength,
-
where, (S(λ)) is given by the height of the source spectrum curve shown below the LCA curve in Figure 2.
-
Simulated polychromatic retinal image was calculated by convoluting the polychromatic PSF with the object image:
 |
Fig. 2 Graphical interpretation of text Equation (3) for computing the polychromatic PSF as the sum of luminance-weighted monochromatic PSFs. For each wavelength in the source spectrum, a monochromatic PSF is computed from monochromatic aberrations plus the focal shift associated with LCA and the lateral displacement associated with TCA; the diagram shows three such PSFs schematically as blur disks of varying diameter. The luminance weighting of each blur disk is given by the height of the source spectrum curve shown below the LCA curve. (Courtesy Ravikumar et al. [(2008 Oct) J. Opt. Soc. Am. A Opt. Image Sci. Vis., 25, 10, 2395–2407]). |
-
where I(x, y) is the simulated retinal image and O(x, y) is the object image.
-
For each simulated retinal image, Strehl ratio and Visual Strehl Ratio computed in frequency domain (VSOTF) was calculated [31].
A preliminary version of Indiana Retinal Image Simulator (IRIS) was used for all the simulations, which implements the various steps detailed above.
2.2 Methodology for simulating random and filtered noise
For simulating the retinal image, wavefront was input into the IRIS software in the form of corresponding Zernike coefficients (Fig. 3). The wavefront was simulated for 6 mm diameter. The signal included the 2–4th Zernike orders, while for simulating noise 7–8th Zernike orders were used. Noise was scaled to predetermined RMS values. All the terms in 5th and 6th Zernike order were set to 0, to avoid overlapping of signal and noise.
 |
Fig. 3 Graphical user interface of the Indiana Retinal Image Simulator (IRIS) used to simulate the polychromatic retinal images. |
For simulating random noise, random Higher Order Aberrations (7th and 8th Zernike Order) were calculated. The same set of Zernike coefficients representing random noise were used in all simulation cases involving random noise, unless mentioned otherwise.
Filtered noise was simulated, using a reticular pattern. The degrees of freedom were amplitude of the signal, spatial frequency and the width of the channel. A grid was calculated for a size of 13X13 mm. Depending on the radial distance, a suitable amplitude factor was used to calculate a transepithelial ablation pattern for this grid, with a central ablation depth of 55 μm, and a peripheral ablation depth of 65 μm. For this calculated transepithelial ablation pattern, for a given spatial frequency, the channel size (signal with a 100% amplitude), and a reticle size (No signal 0% amplitude) was applied as a mask. A randomization factor was added to the pattern to account for the perturbations expected in the real world situations (Fig. 4). As a final step, the ablation pattern was fitted to Zernike polynomials of upto 8th Zernike order with a pupil size of 6 mm. The higher order Zernike polynomials (7th and 8th order coefficients) were scaled to a defined RMS value and used for the simulations. In this manner, the calculated filtered noise mimics the noise associated with a transepithelial ablation pattern allowing spatial frequency as a degree of freedom to manipulate the density of the ablation pattern, in order to simulate the impact on calculated retinal image.
 |
Fig. 4 Left: Example of the filtered noise simulated using a reticular pattern (inset corresponding PSF). Right: The wavefront map reconstructed from the Zernike coefficients obtained after fitting the filtered noise pattern to Zernike Polynomials (up to 8th order), with a fit diameter of 6 mm. |
2.3 Standard settings
The standard values of the input parameters used for all the simulations in the IRIS software are summarized in Table 1. Only one of these input parameter was manipulated at a time, depending on the simulation cases.
The standard values of the input parameters used for all the simulations in the IRIS software. Only one input parameter was manipulated at a time, depending on the simulation cases.
2.4 Simulation cases
The impact of varying degree of roughness, refractive error, pupil diameter, spherical aberrations and spatial frequency of the filtered noise, was individually analyzed on the simulated retinal image through various simulation cases. These cases are summarized in Table 2. For the parameters not mentioned in the Table 2, their standard values were used as described in Table 1.
Settings for different simulation cases for the analyzed metrics.
The simulation case 1 represents purely the impact of chromatic aberrations at 6 mm diameter without the presence of any refractive error. Besides the simulation cases presented in Table 2, further simulations were performed with only filtered noise (no lower order aberrations) of different spatial frequencies (ranging from 0.34 to 1 cycles per mm defined at the cornea plane), but with the RMS of 7th and 8th Zernike order maintained at 0.25 μm. For each analyzed metric, simulation cases were compared based on the simulated retinal image, Strehl Ratio and VSOTF.
3 Results
In total 20 simulation cases were examined and compared on the basis of VSOTF, Strehl Ratio and the simulated retinal image qualitatively.
3.1 Impact of roughness without refractive error
The impact of the roughness without any refractive error is presented in Figures 5 and 6. Without any refractive error, chromatic aberrations resulted in image quality metric VSOTF of ~0.44 and Strehl Ratio of 0.3. Addition of random noise on the signal resulted in deteriorating both VSOTF (from 0.44 no noise to 0.075 with 0.25 μm RMS random noise, and 0.0078 with 0.65 μm RMS random noise) and Strehl Ratio (from 0.3 no noise to 0.03 with 0.25 μm RMS random noise, and 0.005 with 0.65 μm RMS random noise). The decrease in image quality was even worse with the addition of filtered noise.
 |
Fig. 5 Impact of roughness without refractive error on simulated retinal image. Top left: Original object image; Top right: simulated retinal image without refractive error and noise signal; middle left: simulated retinal image without refractive error, with random noise signal (0.25 μm RMS); middle right: simulated retinal image without refractive error and with filtered noise signal (0.25 μm RMS); bottom left: simulated retinal image without refractive error, with random noise signal (0.65 μm RMS); bottom right: simulated retinal image without refractive error and with filtered noise signal (0.65 μm RMS). |
 |
Fig. 6 Impact of roughness (simulated as random and filtered noise) without refractive error on Image quality metrics |
3.2 Impact of roughness with refractive error
The impact of the roughness with refractive errors (Defocus and spherical aberrations) is presented in Figures 7 and 8.
 |
Fig. 7 Impact of roughness with refractive errors (defocus and spherical aberration) on simulated retinal image. Top left: Original object image; Top right: simulated retinal image with refractive error but no noise signal; Bottom Left: simulated retinal image with refractive error and random noise signal; Bottom Right: simulated retinal image with refractive error and filtered noise signal. |
 |
Fig. 8 Impact of roughness (simulated as random and filtered noise) with refractive errors on image quality metrics. |
In the presence of refractive errors of this order (Z[2, 0] = 2 μm and Z[4, 0] = 0.15 μm), adding random noise improved the VSOTF (0.007–0.02) and Strehl Ratio (0.0009–0.005). However, for the filtered noise, the image quality metric VSOTF (0.007–0.002) deteriorated while the Strehl Ratio improved (0.0009–0.006).
3.3 Impact of pupil diameter
Reducing the pupil size resulted in dramatically improving the simulated retinal image without any noise (Strehl Ratio 0.0009, VSOTF 0.007 at 6 mm pupil to 0.018 and 0.03 at 3 mm pupil respectively), and in the presence of random noise (Strehl Ratio 0.005, VSOTF 0.02 at 6 mm pupil to 0.062 and 0.08 at 3 mm pupil respectively). However, for filtered noise, the gains in image quality were marginal in terms of VSOTF (0.002 at 6 mm pupil to 0.0025 at 3 mm pupil), although evident in terms of Strehl Ratio (0.006 at 6 mm pupil to 0.022 at 3 mm pupil) and the image quality in general. These affects are presented in Figures 9 and 10.
 |
Fig. 9 Impact of pupil diameter in the presence of refractive errors (defocus and spherical aberration) on simulated retinal image. Top: simulated retinal image with no noise; middle: simulated retinal image with random noise RMS 0.25 μm at 6 mm diameter; Bottom: Simulated retinal image with filtered noise RMS 0.25 μm at 6 mm diameter. The simulation results with pupil diameter 6 mm are presented in the left column, and pupil diameter 3 mm in the right column. |
 |
Fig. 10 Impact of pupil diameter and roughness (simulated as random and filtered noise) in presence of refractive errors on Image quality metrics. |
3.4 Impact of spherical aberrations
Adding spherical aberrations to the signal results in improving the simulated retinal image quality in the absence of any noise (VSOTF 0.0025 for Z[4, 0] = 0 μm to 0.007 for Z[4, 0] = 0.15 μm), in presence of random noise (VSOTF 0.0132 for Z[4, 0] = 0 μm to 0.02 for Z[4, 0] = 0.15 μm), and also in presence of filtered noise (VSOTF 0.0006 for Z[4, 0] = 0 μm to 0.002 for Z[4, 0] = 0.15 μm). This affect is presented in Figures 11 and 12.
 |
Fig. 11 Impact of spherical aberration in the presence of defocus error on simulated retinal image, with and without the noise signal. Top: simulated retinal image with no noise; middle: simulated retinal image with random noise RMS 0.25 μm at 6 mm diameter; Bottom: Simulated retinal image with filtered noise RMS 0.25 μm at 6 mm diameter. The simulation results with spherical aberrations Z[4, 0] = 0.15 μm are presented in the left column, and spherical aberrations Z[4, 0] = 0 μm in the right column. |
 |
Fig. 12 Impact of spherical aberrations and roughness (simulated as random and filtered noise) in presence of refractive errors on Image quality metrics. |
3.5 Impact of spatial frequency of the filtered noise
Simulations were performed for six different spatial frequencies of the filtered noise pattern (0.34, 0.48, 0.52, 0.67, 0.81, 1 cycles per mm defined at the cornea plane). For each spatial frequency, different set of Zernike coefficients were used, however the RMS of 7th and 8th Zernike order was maintained to 0.25 μm. The impact of spatial frequency on simulated retinal image quality is presented in Figure 13. The image quality metrics VSOTF and Strehl Ratio reached their peaks at the spatial frequency of 0.67 cycle per mm.
 |
Fig. 13 Impact of spatial frequency on simulated retinal image quality. The image quality metrics (VSOTF and Strehl Ratio) reached their peak at the spatial frequency of ~0.67 cycle per mm. |
4 Discussion
Commercially available laser systems used in refractive surgery employ different morphological features, superficial dimensions and contours of the ablations, to induce a defined optical change in a feasible manner [32]. The residual roughness on cornea and other ablation material, after excimer laser ablation has been researched in the past. The routine technique for evaluating the smoothness of an excimer laser keratectomy has been scanning electron microscopy. However, this method suffers from tissue shrinkage and surface artifacts, and evaluates the surface only in a qualitative manner. In a study, a Zygo microscope was used to quantitatively assess the smoothness of the excimer laser ablated corneas, without complicated tissue processing. Significant differences were reported between ablated corneas and PMMA blocks, where ablated corneal surfaces were found rougher than the ablated PMMA surfaces [33].
The temporal and spatial distribution of the laser spots (scan sequence) during a laser ablation procedure has been shown to affect the surface quality and maximum ablation depth of the ablation profile. Mrochen et al. reported that the rough surfaces increase as the amount of temporal overlapping in the scan sequence and the amount of correction increases. The rise in surface roughness was less for bovine corneas than for PMMA in their tests [34]. Doga et al. [35] performed a quantitative evaluation of smoothness of ablation on PMMA using four scanning excimer lasers available commercially for photorefractive surgery. They reported that Scanning excimer lasers based on flying spot technology-Zeiss-Meditec MEL-70 and Microscan, as well as the Nidek EC-5000 CX with FlexScan-created smoother ablations on PMMA plates compared to the older Nidek EC-5000 unit. Similar comparisons on excimer laser delivery systems have been reported in other studies [36, 37].
Hauge et al. [38] examined plane parallel plates of PMMA ablated using two excimer lasers, by the means of focimetry, interferometry, and mechanical surface profiling. Interferometry revealed marked irregularity in the surface of negative corrections, which often had a positive “island” at their center. Positive corrections were generally smoother. These findings were supported by the results of mechanical profiling. Contrast sensitivity measurements carried out when observing through ablated lenses whose power had been neutralized with a suitable spectacle lens of opposite sign confirmed that the surface irregularities of the ablated lenses markedly reduced contrast sensitivity over a range of spatial frequencies. O’Donnell et al. [39] showed that surface irregularities in PMMA increase with ablation depth. They reported that each diopter increment in correction resulted in an approximately 300 nm increased peak-to-valley measurement. This represented an increase of 25 nm roughness per micron of ablation in PMMA. Many of the studies use PMMA as the ablation material of choice due the good correlation between results of laser surface profilometry scans on PMMA and clinical outcomes [40] (and its common use as a calibration material in most laser systems), however, other calibration material have been also proposed and should be equally researched for the aspect of residual roughness [41].
Although published work focuses on comparison of laser delivery methods, beam profiles and calibration materials and their influence on ablation smoothness, an analysis of the impact of residual roughness associated with laser ablation in image modelling has not been extensively pursued. In this work, we proposed a method to convert the residual roughness in ablation to its modelling in polychromatic vision. The residual roughness in the cornea after the laser ablation process was simulated as random or filtered noise added to the wavefront. The signal included the 2–4th Zernike orders, while noise used 7–8th Zernike orders. In order to test the robustness of this method, three different set of randomly generated higher order (7–8th) Zernike coefficients resulting in a RMS of 0.25 μm were fit to a 6 mm fit diameter, and the resulting wavefronts were compared in terms of the simulated retinal image quality and image quality metrics VSOTF and Strehl ratio (Fig. 14). The simulated images were very similar when compared subjectively, and resulted in a comparable Strehl ratio, suggesting the robustness of the employed method in terms of this metric. The metric VSOTF however showed more variations.
 |
Fig. 14 Simulated retinal image and image quality metrics of three wavefronts comprising different set of randomly generated higher order (7–8th) Zernike coefficients as noise (RMS of 0.25 μm) fit to a 6 mm fit diameter. |
The reference wavelength of 550 nm was chosen in our simulations being the peak of human contrast sensitivity, in order to compare the different test settings for the strongest simulated retinal image. However, typically 840 nm is used to measure aberrations in both hartmann shack [42] and Pyramidal sensor1 based aberrometers. Therefore, our results and methods shall be adjusted for this wavelength and for an application with clinically diagnosed aberrations.
In our simulations, the standard settings (Table 1) for defocus was −1.54D (2 μm). This value was selected to have a large enough defocus that shows a detrimental effect in the image quality metrics and modelled images, yet not too large to dominate the impact of Spherical Aberrations and the Higher order aberrations simulating noise. Furthermore, for the majority of patient population for refractive surgery, a myopic correction of −3 to −4D is typically aimed. Considering even the resolution of the detection methods, the simulated value is nearly half of this typical defocus correction. The standard spatial frequency for filtered noise was 0.48 cycles per mm at corneal plane. For a 6 mm pupil size this results in nearly 12 peaks and valleys, fitting to Zernike polynomials of upto 12 orders. However, the simulations were limited upto 8th Zernike orders possible with IRIS. The Stiles-Crawford Sigma was used as proposed by Xu et al. [43]
For all the Wavefronts used in the simulations (with the exception of simulation cases 6 and 7), noise (7–8th Zernike orders) was scaled to a predetermined RMS values of 0.25 μm. This value was selected being the typical value of corneal Higher Order Aberrations (HOAs) at 6 mm for normal eyes [44, 45]. Therefore, the same order of roughness was added to the wavefronts as seen in the natural HOAs. However, it must be noted that the methods presented here, are equally applicable to simulate other levels of corneal roughness. The typical value of ocular spherical aberrations for a 6 mm pupil diameter lies between 0 and 0.1 μm [46]; whereas, the typical value of corneal spherical aberrations lies between 0.2–0.3 μm for a 6 mm pupil diameter [47]. Spherical aberration valuing 0.15 μm was used in the simulation cases, as a compromise close to the typical corneal and ocular values. Our simulations showed an improvement in image quality metrics with the addition of spherical aberrations. This may be originated due to the same sign of defocus and spherical aberrations (both being positive), thus flattening the central part of the wavefront, and improving the central optics in the process.
The quality of simulated retinal image was quantified using the image quality metric VSOTF and Strehl Ratio. The metric visual Strehl calculated using the OTF method (VSOTF) was chosen since it has been reported as the best single – value metric in a study, for predicting how a change in aberration affects high-contrast logMAR visual acuity. The visual Strehl has been shown to account for 81% of the average variance in high-contrast logMAR visual acuity [5]. However, the suitability of VSOTF as an analysis metric for our methods, which is simulation involving higher order aberrations can still be questioned.
The proposed simple and robust method to assess the impact of residual roughness on retinal image, can be utilized in different applications. This method can be applied clinically to different laser platforms based on their associated roughness for choosing a better treatment plan for the patient. Typically, ablations on calibration materials like PMMA are used to calibrate the laser systems. These ablations when analyzed for residual roughness can provide a starting point for the simulations, associated with that laser platform. Applying the methods presented here and using Higher order Zernike coefficients scaled to the typical residual roughness associated with that laser platform, could provide objective retinal image quality metric that can be expected in presence of ablation roughness. Furthermore, the methods can be used for computing realistic image quality metrics for the patient’s postoperative vision. However, it must be noted that subjective image perception and simulated optical image quality can be different. There are several factors like the image perception by the brain [4], and epithelium masking after refractive surgery [48] which cannot be easily simulated. In a study involving 15 eyes of 15 patients who underwent LASIK, patients were examined for upto 2 years postoperatively [49]. The total corneal thickness remained unaltered, but epithelial hyperplasia was seen at 2 years. Keratocyte density in the anterior stroma and posterior to the flap interface showed a slight decrease during the follow-up. Subbasal nerve density decreased 82% in 5 days after LASIK. In these eyes, corneal remodelling seemed to continue for at least 2 years. Kanellopoulos and Asimellis [50] explained their findings of epithelial thickening after myopic LASIK with their hypothesis that epithelial behavior is related to the biomechanics of the cornea and that a thinned cornea (in cases of large myopic ablation) might be more susceptible to epithelial hyperactivity and regrowth. Conversely, Reinstein et al. [51] suggested that all epithelial thickness changes can be explained by a compensatory mechanism that is driven by the rate of change of curvature of the stromal surface. Vinciguerra et al. [52, 53] demonstrated that the initial curvature gradient after excimer ablation predicts the change in tangential curvature over the subsequent 12 months in areas where the initial tangential curvature is the greatest. When the curvature gradient is high, the surface curvature modification remains in progress even months after the ablation.
Furthermore, it is known that stromal topography affects overlaying epithelial function including the differential expression of both cellular and extracellular substances [54]. For a re-growing epithelium affected by laser cuts, the balance between the pressure exerted by the superficial cell layer under tension and the epithelial growth pressure might be the factor determining the thickness of the epithelium at any point of the cornea in steady state conditions [55]. Several other factors have also been identified to be associated with an increase in epithelial thickness, like small ablation zones, greater attempted corrections, and a greater rate of change in power at the edge of the ablation zone. Larger, smoother ablation profiles may result in less epithelial hyperplasia [56]. Although the corneal wound healing response is exceedingly complex, quantitative models of corneal surface smoothing after laser ablation for refractive correction, have been proposed in the past [57, 58]. Our methods did not account for epithelial masking and regrowth in assuaging the residual roughness after corneal ablation, and hence affecting the simulated retinal image. This can be regarded as a limitation to our methods.
There are several challenges associated to the analysis of polychromatic images. Wavefront aberration maps are usually only available for just one wavelength, depending on the wavelength of the aberrometer. Therefore, a conversion of wavefront aberration to another wavelengths is necessary for an analysis. Furthermore, convolution approaches can be only utilized for light sources which are spectrally homogenous. For evaluating the impact of aberrations on polychromatic images, a hyperspectral analysis is required. Additionally, the sampling frequency of the spectral power distributions (of image) and pupil functions should be matched. These measures were accounted, however, our methods still present some limitations. We used Zernike coefficients of 7–8th order to simulate noise. This can be conceptually acceptable for simulating random noise, but filtered noise simulated through these Zernike orders may be too coarse compared to the reality. An ideal solution would have been to include more Zernike orders for simulation or to add the filtered noise as a raw (elevation) map, on to the wavefront signal, however, both strategies were not possible in the simulation software (IRIS). Nevertheless, the simulation results for filtered noise can be still considered for comparison to the random noise. The scale of the roughness shall be analysed before applying our methods clinically. If the scale of the roughness being analyzed is small compared to the spacing of lenslets in aberrometer sensor, the measured roughness (RMS HOA) and hence the simulated retinal image cannot be trusted.
5 Conclusion
Despite the limitations, the proposed method enables quantifying the impact of residual roughness in corneal ablation processes at a relatively low cost. Since normally laser ablation is an integral process divided on a defined grid, the impact of spatially characterized noise represents a more realistic simulation condition. This method can help comparing different refractive laser platforms in terms of their associated roughness in ablation, indirectly improving the quality of results after Laser vision correction surgery.
Competing interests
The authors have no financial or proprietary interest in a product, method, or material described herein.
But authors Shwetabh Verma and Samuel Arba Mosquera are employees at SCHWIND eye-tech-solutions, Kleinostheim, Germany. The article represents the personal views of these Authors, and was not written as a work for hire within the terms of the Author’s employment with SCHWIND eye-tech-solutions. The work described in the article itself (as opposed to the work done writing the article) was conducted as part of the Author’s work for SCHWIND Eye-Tech-Solutions. Content attributed to the Authors was vetted by a standard SCHWIND eye-tech-solutions approval process for third-party publications.
Juergen Hesser reports no conflict of interest.
Preliminary version of this work has been presented at European Association for Vision and Eye Research (EVER) 2017 and The Association for Research in Vision and Ophthalmology (ARVO) 2018.
Funding
The authors received financial support from ZIM (Zentrales Innovationsprogramm Mittelstand, Germany) BMWI (reference number ZF4340402AK7) for partially supporting this research work.
Availability of data and materials
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Authors’ contributions
Shwetabh Verma made substantial contributions to conception and design, acquisition of data, analysis and interpretation of results. He was involved in drafting the manuscript, and final approval of the version to be published.
Jürgen Hesser made substantial contributions in analysis and interpretation of results, and critically revising the manuscript for important intellectual content. He was involved in final approval of the version to be published.
Samuel Arba Mosquera made substantial contributions to conception and design, in analysis and interpretation of results, and critically revising the manuscript for important intellectual content. He was involved in final approval of the version to be published.
Acknowledgments
Mr. Mateusz Jaskulski supported this work with a preliminary version of the Indiana Retinal Image Simulator (Jaskulski M, Thibos L, Bradley A, Kollbaum P, et al. IRIS – Indiana Retinal Image Simulator. 2019; https://blogs.iu.edu/corl/iris).
References
- Watson A.B., Ahumada A.J. (2012) Modeling acuity for optotypes varying in complexity, J. Vision 12, 10, 1–19. [Google Scholar]
- Watson A.B., Ahumada A.J. Jr (2008) Predicting visual acuity from wavefront aberrations, J. Vision 8, 4, 17. [Google Scholar]
- Thibos L.N., Applegate R.A., Schwiegerling J.T., Webb R. (2002) Standards for reporting the optical aberrations of eyes, J. Refract. Surg. 18, 5, S652–S660. [Google Scholar]
- Watson A.B., Ahumada A.J. (2015) Letter identification and the neural image classifier, J. Vision 15, 2, 15. [Google Scholar]
- Marsack J.D., Thibos L.N., Applegate R.A. (2004) Metrics of optical quality derived from wave aberrations predict visual performance, J. Vision 4, 322–328. [Google Scholar]
- Marcos S., Barbero S., Llorente L., Merayo-Lloves J. (2001) Optical response to LASIK surgery for myopia from total and corneal aberration measurements, Invest. Ophthalmol. Visual Sci. 42, 3349–3356. [Google Scholar]
- Applegate R.A., Marsack J.D., Thibos L.N. (2006) Metrics of retinal image quality predict visual performance in eyes with 20/17 or better visual acuity, Optom. Vision Sci. 83, 635–640. [CrossRef] [Google Scholar]
- Cheng X., Bradley A., Thibos L.N. (2004) Predicting subjective judgment of best focus with objective image quality metrics”, J. Vision 4, 310–321. [Google Scholar]
- Chen L., Singer B., Guirao A., Porter J., Williams D.R. (2005) Image metrics for predicting subjective image quality, Optom. Vision Sci. 82, 358–369. [CrossRef] [Google Scholar]
- Marcos S., Burns S.A., Moreno-Barriusop E., Navarro R. (1999) A new approach to the study of ocular chromatic aberrations, Vision Res. 39, 4309–4323. [CrossRef] [Google Scholar]
- Ravikumar S., Bradley A., Thibos L.N. (2006) Do monochromatic aberrations protect the eye against chromatic blur?, Invest. Ophthalmol. Visual Sci. 47, EAbstract 1505. [Google Scholar]
- van Meeteren A. (1974) Calculations on the optical modulation transfer function of the human eye for white light, Opt. Acta 21, 395–412. [NASA ADS] [CrossRef] [Google Scholar]
- Marcos S., Burns S.A., Moreno-Barriusop E., Navarro R. (1999) A new approach to the study of ocular chromatic aberrations, Vision Res. 39, 4309–4323. [CrossRef] [Google Scholar]
- Ravikumar S., Thibos L.N., Bradley A. (2008 Oct) Calculation of retinal image quality for polychromatic light, J. Opt. Soc. Am. A Opt. Image Sci. Vis. 25, 10, 2395–407. [NASA ADS] [CrossRef] [Google Scholar]
- Arines J., Almaguer C., Acosta E. (2017) Potential use of cubic phase masks for extending the range of clear vision in presbyopes: Initial calculation and simulation studies, Opht. Phys. Opt. 37, 2, 141–150. https://doi.org/10.1111/opo.12348. [CrossRef] [Google Scholar]
- Águila-Carrasco A.J., Read S.A., Montés-Micó R., Iskander D.R. (2017) The effect of aberrations on objectively assessed image quality and depth of focus, J. Vision 17, 2, 2. https://doi.org/10.1167/17.2.2. [CrossRef] [Google Scholar]
- Young L.K., Love G.D., Smithson H.E. (2013) Accounting for the phase, spatial frequency and orientation demands of the task improves metrics based on the visual Strehl ratio, Vision Res. 90, 57–67. [CrossRef] [Google Scholar]
- Verma S., Hesser J., Arba-Mosquera S. (2017) Optimum laser beam characteristics for achieving smoother ablations in laser vision correction, Invest. Ophthalmol. Vis. Sci. 58, 4, 2021–2037. [CrossRef] [Google Scholar]
- Thomas J.W., Mitra S., Chuang A.Z., Yee R.W. (2003) Electron microscopy of surface smoothness of porcine corneas and acrylic plates with four brands of excimer laser, J. Refract. Surg. 19, 6, 623–8. [CrossRef] [Google Scholar]
- Verma S., Hesser J., Arba-Mosquera S. (2021) Effect of laser beam truncation (pinhole), (ordered) dithering, and jitter on residual smoothness after poly(methyl methacrylate) ablations, using a close-to-Gaussian beam profile, Adv. Opt. Technol. 10, 6, 409–421. https://doi.org/10.1515/aot-2021-0040. [NASA ADS] [CrossRef] [Google Scholar]
- Vinciguerra P., Camesasca F.I., Vinciguerra R., Arba-Mosquera S., Torres I., Morenghi E., Randleman J.B. (2017) Advanced surface ablation with a new software for the reduction of ablation irregularities, J. Refract. Surg. 33, 2, 89–95. https://doi.org/10.3928/1081597X-20161122-01. PMID: 28192587. [CrossRef] [Google Scholar]
- Naroo S.A., Charman W.N. (2005) Surface roughness after excimer laser ablation using a PMMA model: Profilometry and effects on vision, J. Refract. Surg. 21, 3, 260–8. [CrossRef] [Google Scholar]
- Vinciguerra P., Azzolini M., Radice P., Sborgia M., De Molfetta V. (1998) A method for examining surface and interface irregularities after photorefractive keratectomy and laser in situ keratomileusis: Predictor of optical and functional outcomes, J. Refract. Surg. 14, 2 Suppl, S204–6. [Google Scholar]
- Walker M.B., Wilson S.E. (2001) Recovery of uncorrected visual acuity after laser in situ keratomileusis or photorefractive keratectomy for low myopia, Cornea 20, 2, 153–5. [CrossRef] [Google Scholar]
- Hersh P.S., Brint S.F., Maloney R.K., Durrie D.S., Gordon M., Michelson M.A., Thompson V.M., Berkeley R.B., Schein O.D., Steinert R.F. (1998) Photorefractive keratectomy versus laser in situ keratomileusis for moderate to high myopia. A randomized prospective study, Ophthalmology 105, 8, 1512–22. discussion 1522–3. [CrossRef] [Google Scholar]
- Lin D.T.C., Holland S.P., Verma S., Hogden J., Arba-Mosquera S. (2019) Immediate and short term visual recovery after SmartSurfACE photorefractive keratectomy, J. Optom. 12, 4, 240–247. https://doi.org/10.1016/j.optom.2019.04.003. Epub 2019 Aug 28. PMID: 31473174; PMCID: PMC6978587. [CrossRef] [Google Scholar]
- de Ortueta D., von Rüden D., Arba-Mosquera S. (2022) Refractive effect of epithelial remodelling in myopia after transepithelial photorefractive keratectomy, Vision 6, 4, 74. https://doi.org/10.3390/vision6040074. [CrossRef] [Google Scholar]
- Vinciguerra P., Azzolini M., Airaghi P., Radice P., De Molfetta V. (1998) Effect of decreasing surface and interface irregularities after photorefractive keratectomy and laser in situ keratomileusis on optical and functional outcomes, J. Refract. Surg. 14, 2 Suppl, S199–203. [Google Scholar]
- Howarth P.A., Zhang X., Bradley A., Still D.L., Thibos L.N. (1988) Does the chromatic aberration of the eye vary with age?, Vision Res. 5, 2087–2092. [Google Scholar]
- Salmon T.O., West R.W., Gasser W., Kenmore T. (2003) Measurement of refractive errors in young myopes using the COAS Shack-Hartmann aberrometer, Optom. Vis. Sci. 80, 1, 6–14. [CrossRef] [Google Scholar]
- Thibos L.N., Hong X., Bradley A., Applegate R.A. (2004) Accuracy and precision of objective refraction from wavefront aberrations, J. Vision 4, 4, 329–51. [Google Scholar]
- Canals M., Elies D., Costa-Vila J., Coret A. (2004) Comparative study of ablation profiles of six different excimer lasers, J. Refract. Surg. 20, 2, 106–9. [CrossRef] [Google Scholar]
- Liang F.Q., Geasey S.D., del Cerro M., Aquavella J.V. (1992) A new procedure for evaluating smoothness of corneal surface following 193-nanometer excimer laser ablation, Refract. Corneal Surg. 8, 6, 459–65. [Google Scholar]
- Mrochen M., Schelling U., Wuellner C., Donitzky C. (2009) Influence of spatial and temporal spot distribution on the ocular surface quality and maximum ablation depth after photoablation with a 1050 Hz excimer laser system, J. Cataract Refract. Surg. 35, 2, 363–73. https://doi.org/10.1016/j.jcrs.2008.10.053. [CrossRef] [Google Scholar]
- Doga A.V., Shpak A.A., Sugrobov V.A. (2004) Smoothness of ablation on polymethylmethacrylate plates with four scanning excimer lasers, J. Refract. Surg. 20, 5 Suppl, S730–3. [Google Scholar]
- Argento C., Valenzuela G., Huck H., Cremona G., Cosentino M.J., Gale M.F. (2001) Smoothness of ablation on acrylic by four different excimer lasers, J. Refract. Surg. 17, 1, 43–5. [CrossRef] [Google Scholar]
- O’Donnell C.B., Kemner J., O’Donnell F.E. Jr (1996) Ablation smoothness as a function of excimer laser delivery system, J. Cataract Refract. Surg. 22, 6, 682–5. [CrossRef] [Google Scholar]
- Hauge E., Naroo S.A., Charman W.N. (2001) Poly(methyl methacrylate) model study of optical surface quality after excimer laser photorefractive keratectomy, J Cataract Refract Surg. 27, 12, 2026–35. [CrossRef] [Google Scholar]
- O’Donnell C.B., Kemner J., O’Donnell F.E. (1996) Surface roughness in PMMA is linearly related to the amount of excimer laser ablation, J. Refract. Surg. 12(1), 171–4. [CrossRef] [Google Scholar]
- Anschutz T., Pieger S. (1999) Correlation of laser profilometry scans with clinical results, J. Refract. Surg. 15, 2 Suppl, S252–6. [Google Scholar]
- Arba-Mosquera S., Vinciguerra P., Verma S. (2018) Review of technological advancements in calibration systems for laser vision correction, J. Biomed. Opt. 23, 2, 1–8. [CrossRef] [Google Scholar]
- Salmon T.O., West R.W., Gasser W., Kenmore T. (2003) Measurement of refractive errors in young myopes using the COAS Shack-Hartman n aberrometer, Optom. Vis. Sci. 80, 1, 6–14. [CrossRef] [Google Scholar]
- Xu R., Bradley A., Thibos L.N. (2013) Impact of primary spherical aberration, spatial frequency and Stiles Crawford apodization on wavefront determined refractive error: A computational study, Ophthal. Physiol. Opt. 33, 4, 444–55. https://doi.org/10.1111/opo.12072. Epub 2013 May 19. PMID: 23683093; PMCID: PMC4056778. [CrossRef] [Google Scholar]
- Zhao P.F., Li S.M., Lu J., Song H.M., Zhang J., Zhou Y.H., Wang N.L. (2017) Effects of higher-order aberrations on contrast sensitivity in normal eyes of a large myopic population, Int. J. Ophthalmol. 10, 9, 1407–1411. [Google Scholar]
- Domínguez-Vicent A., Pérez-Vives C., Ferrer-Blasco T., García-Lázaro S., Montés-Micó R. (2013) The effect of simulated normal and amblyopic higher-order aberrations on visual performance, J. AAPOS 17, 3, 269–75. [CrossRef] [Google Scholar]
- Shetty N., Kochar S., Paritekar P., Artal P., Shetty R., Nuijts R.M.M.A., Webers C.A.B., Sinha Roy A. (2018) Patient-specific determination of change in ocular spherical aberration to improve near and intermediate visual acuity of presbyopic eyes, J. Biophoton. 12, 4, e201800259. [Google Scholar]
- Arba Mosquera S., de Ortueta D. (2011) Correlation among ocular spherical aberration, corneal spherical aberration, and corneal asphericity before and after LASIK for myopic astigmatism with the SCHWIND AMARIS platform, J. Refract. Surg. 27, 6, 434–43. [Google Scholar]
- Lohmann C.P., Guell J.L. (1998) Regression after LASIK for the treatment of myopia: The role of the corneal epithelium, Semin. Ophthalmol. 13, 2, 79–82. [Google Scholar]
- Moilanen J.A., Holopainen J.M., Vesaluoma M.H., Tervo T.M. (2008) Corneal recovery after LASIK for high myopia: A 2-year prospective confocal microscopic study, Br. J. Ophthalmol. 92, 10, 1397–402. https://doi.org/10.1136/bjo.2007.126821. [CrossRef] [Google Scholar]
- Kanellopoulos A.J., Asimellis G. (2014) Longitudinal postoperative LASIK epithelial thickness profile changes in correlation with degree of myopia correction, J. Refract. Surg. 30, 166–171. https://doi.org/10.3928/1081597X-20140217-03. [Google Scholar]
- Reinstein D.Z., Archer T.J., Gobbe M. (2014) Rate of change of curvature of the corneal stromal surface drives epithelial compensatory changes and remodeling, J. Refract. Surg. 30, 800–802. https://doi.org/10.3928/1081597X-20141113-02. [CrossRef] [Google Scholar]
- Vinciguerra P., Azzolini C., Vinciguerra R. (2015) Corneal curvature gradient determines corneal healing process and epithelial behavior, J. Refract. Surg. 31, 4, 281–2. https://doi.org/10.3928/1081597X-20150319-08. [CrossRef] [Google Scholar]
- Vinciguerra P., Roberts C.J., Albé E., Romano M.R., Mahmoud A., Trazza S., Vinciguerra R. (2014) Corneal curvature gradient map: A new corneal topography map to predict the corneal healing process, J. Refract. Surg. 30, 3, 202. [CrossRef] [Google Scholar]
- Wilson S.E., Mohan R.R., Hong J.W., Lee J.S., Choi R., Mohan R.R. (2001) The wound healing response after laser in situ keratomileusis and photorefractive keratectomy: Elusive control of biological variability and effect on custom laser vision correction, Arch. Ophthalmol. 119, 6, 889–96. [CrossRef] [Google Scholar]
- Dierick H.G., Missotten L. (1992) Is the corneal contour influenced by a tension in the superficial epithelial cells? A new hypothesis, Refract. Corneal Surg. 8, 1, 54–9; discussion 60. [Google Scholar]
- Gauthier C.A., Holden B.A., Epstein D., Tengroth B., Fagerholm P., Hamberg-Nyström H. (1997) Factors affecting epithelial hyperplasia after photorefractive keratectomy [see comments], J. Cataract Refract. Surg 23, 7, 1042–50. [CrossRef] [Google Scholar]
- Huang D., Tang M., Shekhar R. (2003) Mathematical model of corneal surface smoothing after laser refractive surgery, Am. J. Ophthalmol. 135, 3, 267–78. [CrossRef] [Google Scholar]
- Lieberman D.M., Grierson J.W. (2000) A mathematical model for laser in situ keratomileusis and photorefractive keratectomy, J. Refract. Surg. 16, 2, 177–86. [CrossRef] [Google Scholar]
All Tables
The standard values of the input parameters used for all the simulations in the IRIS software. Only one input parameter was manipulated at a time, depending on the simulation cases.
All Figures
 |
Fig. 1 Schematic representation of how the roughness is induced during the pulse-by-pulse ablation process – exaggerated scale. The letters correspond to arbitrary areas (in yellow) in which the residual ablation is evaluated, whereas numbers represent individual laser pulses. The thick horizontal line represents the target ideal surface (without any roughness). |
| In the text | |
 |
Fig. 2 Graphical interpretation of text Equation (3) for computing the polychromatic PSF as the sum of luminance-weighted monochromatic PSFs. For each wavelength in the source spectrum, a monochromatic PSF is computed from monochromatic aberrations plus the focal shift associated with LCA and the lateral displacement associated with TCA; the diagram shows three such PSFs schematically as blur disks of varying diameter. The luminance weighting of each blur disk is given by the height of the source spectrum curve shown below the LCA curve. (Courtesy Ravikumar et al. [(2008 Oct) J. Opt. Soc. Am. A Opt. Image Sci. Vis., 25, 10, 2395–2407]). |
| In the text | |
 |
Fig. 3 Graphical user interface of the Indiana Retinal Image Simulator (IRIS) used to simulate the polychromatic retinal images. |
| In the text | |
 |
Fig. 4 Left: Example of the filtered noise simulated using a reticular pattern (inset corresponding PSF). Right: The wavefront map reconstructed from the Zernike coefficients obtained after fitting the filtered noise pattern to Zernike Polynomials (up to 8th order), with a fit diameter of 6 mm. |
| In the text | |
 |
Fig. 5 Impact of roughness without refractive error on simulated retinal image. Top left: Original object image; Top right: simulated retinal image without refractive error and noise signal; middle left: simulated retinal image without refractive error, with random noise signal (0.25 μm RMS); middle right: simulated retinal image without refractive error and with filtered noise signal (0.25 μm RMS); bottom left: simulated retinal image without refractive error, with random noise signal (0.65 μm RMS); bottom right: simulated retinal image without refractive error and with filtered noise signal (0.65 μm RMS). |
| In the text | |
 |
Fig. 6 Impact of roughness (simulated as random and filtered noise) without refractive error on Image quality metrics |
| In the text | |
 |
Fig. 7 Impact of roughness with refractive errors (defocus and spherical aberration) on simulated retinal image. Top left: Original object image; Top right: simulated retinal image with refractive error but no noise signal; Bottom Left: simulated retinal image with refractive error and random noise signal; Bottom Right: simulated retinal image with refractive error and filtered noise signal. |
| In the text | |
 |
Fig. 8 Impact of roughness (simulated as random and filtered noise) with refractive errors on image quality metrics. |
| In the text | |
 |
Fig. 9 Impact of pupil diameter in the presence of refractive errors (defocus and spherical aberration) on simulated retinal image. Top: simulated retinal image with no noise; middle: simulated retinal image with random noise RMS 0.25 μm at 6 mm diameter; Bottom: Simulated retinal image with filtered noise RMS 0.25 μm at 6 mm diameter. The simulation results with pupil diameter 6 mm are presented in the left column, and pupil diameter 3 mm in the right column. |
| In the text | |
 |
Fig. 10 Impact of pupil diameter and roughness (simulated as random and filtered noise) in presence of refractive errors on Image quality metrics. |
| In the text | |
 |
Fig. 11 Impact of spherical aberration in the presence of defocus error on simulated retinal image, with and without the noise signal. Top: simulated retinal image with no noise; middle: simulated retinal image with random noise RMS 0.25 μm at 6 mm diameter; Bottom: Simulated retinal image with filtered noise RMS 0.25 μm at 6 mm diameter. The simulation results with spherical aberrations Z[4, 0] = 0.15 μm are presented in the left column, and spherical aberrations Z[4, 0] = 0 μm in the right column. |
| In the text | |
 |
Fig. 12 Impact of spherical aberrations and roughness (simulated as random and filtered noise) in presence of refractive errors on Image quality metrics. |
| In the text | |
 |
Fig. 13 Impact of spatial frequency on simulated retinal image quality. The image quality metrics (VSOTF and Strehl Ratio) reached their peak at the spatial frequency of ~0.67 cycle per mm. |
| In the text | |
 |
Fig. 14 Simulated retinal image and image quality metrics of three wavefronts comprising different set of randomly generated higher order (7–8th) Zernike coefficients as noise (RMS of 0.25 μm) fit to a 6 mm fit diameter. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![$$ \mathrm{PSF}\left(x,y\right)={\left|\mathrm{FT}\left[P(x,y)\bullet {e}^{\frac{i2\pi }{\lambda }W(x,y)}\right]\right|}^2. $$](/articles/jeos/full_html/2023/01/jeos20220036/jeos20220036-eq2.gif)