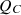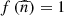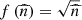EDP Sciences logo
Submit your research paper
Search
Menu
All issues Volume 19 / No 2 (2023) J. Eur. Opt. Society-Rapid Publ., 19 2 (2023) 42 Full HTML
Open Access
Issue
J. Eur. Opt. Society-Rapid Publ.
Volume 19, Number 2, 2023
Article Number 42
Number of page(s) 5
DOI https://doi.org/10.1051/jeos/2023039
Published online 07 November 2023

© The Author(s), published by EDP Sciences, 2023

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

The most widely applied model in the study of quantum optics is the Jaynes–Cummings model [1]. It explains how an atom interacts with a quantized electromagnetic field. It describes the interaction of an atom with a radiation field. A broad framework for a 2-level atom interacting with a single-mode field with the concept of nonlinearities has been developed [2]. The interaction of an atom with a 2-mode cavity field has been investigated [3–5]. The interaction between a 3-level atom, with Ξ, Λ and V configurations, and 1- or 2-mode field was examined [6–8]. The 4-level atoms under various configurations have received attention recently and their interactions with cavity modes. In this context, several 4-level atomic system schemes have been illustrated and analyzed [9–14]. The interaction between a 5-level system in different configurations (M and K-type) has attracted attention in quantum optics. Several optical phenomena have been analyzed. The spontaneous emission in a four-field-driven, five-level atomic system have been explored [15]. The decoherence effect in the 5-level atom systems has been studied [16–18]. More recently, an atomic system with six levels in the existence of a radiation field is considered [19].

Many quantum phenomena have been produced as resources for carrying out numerous tasks in the field of quantum optics and information, both theoretically and practically [20–23]. This development took place over the course of a few years. In most cases, the coherent superposition of quantum states is regarded as an essential need for the existence of quantum correlations [24–30]. The idea of the EPR paradox [31] that was presented by Einstein, Podolsky, and Rosen was the impetus behind the establishment of this precondition. It invoked how the theory of quantum physics enables spooky activity at a distance Schrödinger viewed the problem as one in which it was possible for local observations to influence a distant system even without having access to it [32]. After that, Bell came up with the so-called Bell inequality as a way to illustrate that this “spooky” phenomenon was not a coincidence. Subsequently, Bell presented the so-called Bell inequality to demonstrate that this “spooky activity” causes a quantum correlation that defies any classical explanation [33]. This was done in order to prove that the existence of this quantum correlation cannot be explained using conventional methods. Quantum coherence is the fundamental concept that underpins a variety of quantum phenomena that occur in nanomaterials [34, 35], quantum measurements and quantum metrology [36–40], and applications of quantum mechanics to biology [41–43]. According to the underlying meaning of quantum coherence, it was not until recently that an accurate theory of coherence was emphasized with the constraints necessary to ensure that quantum coherence is a physical resource [44]. This was done in light of the fact that quantum coherence has been given increasing attention in recent years. As a result, many quantum measures that check these limitations have been developed, most notably those that are based on the 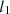l 1 $ {l}_1$ norm and relative entropy [44]. In addition, the quantum coherence may be measured by either the convex-roof construction or nonlocal correlation [45, 46], and an operational theory of coherence has been developed [47].

Quantum entanglement is the aspect of a composite quantum system that most captivates our attention as a fascinating occurrence. If the combined state of two particles cannot be represented as a product of the states of their constituent subsystems, then the particles are said to be entangled [31]. A deeper comprehension of fundamental quantum processes may be attained through the production and manipulation of these entangled states. Examples of complicated entangled states that are utilized in tests of quantum nonlocality include triplets of particles named after Greenberger et al. and Pan et al. [48, 49]. In addition to these fundamental qualities, entanglement has developed into a crucial resource in quantum information processing, which is a field that has made significant strides in the past few years [50, 51].

Motivated by the recent development of atom-field system in quantum optics, we analyze the interaction between a SLAS and 1-mode field initially in squeezed coherent states. The field has one mode and the interaction is affected by five photons. We extend the Jeans–Cummings model to describe the interaction between the atom and the SF and the system dynamics. We analyze the time evolution of the atomic coherence, non-local correlation, statistical properties within the bipartite system in the presence and absence of intensity-dependent coupling for different squeezing regimes of the field. A full understanding of the dynamics of atomic systems that interact with a quantized field is becoming crucial, especially with respect to applications for quantum optics and information science. To implement the quantum computer the most important ingredient is the quantum dynamics, in which one subsystem undergoes a coherent evolution that depends on the state of another subsystem.

The present manuscript is outlined as follows: In Section 2, we present the model which describes SLAS in a cascade type interacting with a quantized field initially defined in a SF. Section 3 describes the quantumness measures and the main results. Finally, a summary and conclusions are illustrated in the last section.

2 Physical model and wave function

Here, we introduce the quantum scheme of a SLAS interacting with a nonlinear field. The SLAS is considered with transition energy between the six levels ωj (j = 1,…, 6) where ω1 > ω2 > .... > ω6. The SLAS states |j〉 are ordered from the upper state |1〉 to the lower state |6〉. We assume that the SLAS begins in its upper state and that the field in the squeezed coherent states (SCS) denoted by |α, r〉. The state of the system at = 0 is |U(0)〉 = |α, r, 1〉 and the state |α, r〉 is defined by [52]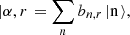 | α , r 〉 = ∑ n b n , r | n 〉 , $$ \left|\alpha,r\right.\rangle=\sum_n {b}_{n,r}\left|\mathrm{n}\right.\rangle, $$(1)where r is the squeezed parameter and the amplitude bn,r is given by 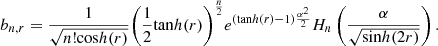  b n , r = 1 n ! cos h ( r ) ( 1 2 tan h ( r ) ) n 2 e ( tan h ( r ) - 1 ) α 2 2 H n ( α sin h ( 2 r ) ) . $$ {\enspace b}_{n,r}=\frac{1}{\sqrt{n!\mathrm{cos}h(r)}}{\left(\frac{1}{2}\mathrm{tan}h(r)\right)}^{\frac{n}{2}}{e}^{\left(\mathrm{tan}h(r)-1\right)\frac{{\alpha }^2}{2}}{H}_n\left(\frac{\alpha }{\sqrt{\mathrm{sin}h(2r)}}\right). $$(2)

The interaction Hamiltonian can be expressed as [1] H ̂ I = ∑ j = 1 5 λ j [ | j 〉 〈 j + 1 | f ( a ̂ † a ̂ ) a ̂ + a ̂ † f ( a ̂ † a ̂ ) | j + 1 〉 〈 j | ] , $$ {\widehat{H}}_I=\sum_{j=1}^5 {\lambda }_j\left[|j\right\rangle\left\langle j+1|f({\widehat{a}}^{\dagger }\widehat{a})\widehat{a}+{\widehat{a}}^{\dagger }f({\widehat{a}}^{\dagger }\widehat{a})|j+1\right\rangle\left\langle j|\right], $$(3)where f ( a ̂ † a ̂ )   $ 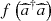f\left({\widehat{a}}^{\dagger }\widehat{a}\right)\enspace $represents an arbitrary intensity-dependent atom-field coupling, and λj designs the atom-field coupling constant, and we focus here on the case of identical coupling with ξj = λj+1 = λ, j = 1…4.

The SLAS-field wave function at t > 0 and ξt being the scaled time can be formulated as: | Ψ ( t ) 〉 = ∑ n b n , r [ ∑ J = 1 6 A j ( t ) | n + j - 1 〉 ⊗ | j 〉 ] . $$ |\mathrm{\Psi }(t)\rangle=\sum_n {b}_{n,r}\left[\sum_{J=1}^6 {A}_j(t)|n+j-1\rangle\otimes |j\rangle\right]. $$(4)

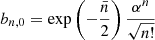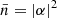In the case of absence of the squeezing (i.e. r = 0), the field is in the coherent state and b n , 0 = exp ( - n ̅ 2 ) α n n ! $ {b}_{n,0}=\mathrm{exp}\left(-\frac{\bar{n}}{2}\right)\frac{{\alpha }^n}{\sqrt{n!}}$, and n ̅ = | α | 2   $ \bar{n}=|\alpha {|}^2\enspace $is the initial mean photon number of the field-mode. 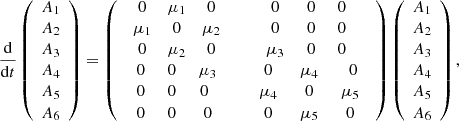With the help of Schrödinger equation and applying the Hamiltonian (3) on the state ket (4), we have d d t ( A 1 A 2 A 3 A 4 A 5 A 6 ) = ( 0 μ 1 0 μ 1 0 μ 2 0 μ 2 0 0   0   0 0   0   0 μ 3   0   0 0   0   μ 3 0   0 0 0   0   0   0 μ 4   0 μ 4 0 μ 5 0   μ 5   0 ) ( A 1 A 2 A 3 A 4 A 5 A 6 ) , $$ \frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{A}_1\\ {A}_2\\ {A}_3\\ {A}_4\\ {A}_5\\ {A}_6\end{array}\right)=\left(\begin{array}{cc}\begin{array}{ccc}0& {\mu }_1& 0\\ {\mu }_1& 0& {\mu }_2\\ 0& {\mu }_2& 0\end{array}& \begin{array}{ccc}0& \enspace 0& \enspace 0\\ 0& \enspace 0& \enspace 0\\ {\mu }_3& \enspace 0& \enspace 0\end{array}\\ \begin{array}{ccc}0& \enspace 0& \enspace {\mu }_3\\ 0& \enspace 0& 0\\ 0& \enspace 0& \enspace 0\end{array}& \enspace \begin{array}{ccc}0& {\mu }_4& \enspace 0\\ {\mu }_4& 0& {\mu }_5\\ 0& \enspace {\mu }_5\enspace & 0\end{array}\end{array}\right)\left(\begin{array}{c}{A}_1\\ {A}_2\\ {A}_3\\ {A}_4\\ {A}_5\\ {A}_6\end{array}\right), $$(5)where μ j = - i λ   ( n + j )   $ {\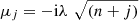mu }_j=-\mathrm{i}\lambda \enspace \sqrt{\left(n+j\right)}\enspace $in the case of absence of the I-DC and μ j = - i λ   ( n + j ) $ {\mu }_j=-\mathrm{i}\lambda \enspace \left(n+j\right)$ under the I-DC effect for f ( a ̂ † a ̂ ) = a ̂ † a ̂ . 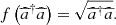$ f\left({\widehat{a}}^{\dagger }\widehat{a}\right)=\sqrt{{\widehat{a}}^{\dagger }\widehat{a}}.$

3 Quantum quantifiers and numerical results

3.1 Atomic quantum entropy

Here, we provide a brief description of the von Neumann entropy, quantum coherence, and nonclassical features of the radiation field based on the variation of the Mandel parameter.

In this manuscript, the SLAS-SF entanglement can be detected through the von Neumann according to the atomic basis or field basis. For a quantum system, the von Neumann entropy is determined by [53]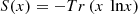 S ( x ) = - Tr ( x   ln x ) $$ S(x)=-{Tr}\left(x\enspace \mathrm{ln}x\right) $$(6)where x is the density operator describing the given quantum state that gives zero for all pure states with x 2 = x. In our case, it can be written as a function of the eigenvalues SLAS density matrix S SF = S S LAS = - ∑ j ζ j ln ζ j . 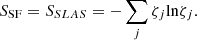$$ {S}_{\mathrm{SF}}={S}_{S{LAS}}=-\sum_j {\zeta }_j\mathrm{ln}{\zeta }_j. $$(7)

Let us now analyze the effect of the system parameters on the dynamics of the quantum entanglement of the SLAS-SF state. In Figure 1, for a SLAS initially in an upper quantum state and the quantized field in SF, we depict the time variation of the function SSLAS against the normalized time λt in the absence and presence of squeezing and I-DC effect. Generally, we can see that the entanglement measure exhibits an oscillator behavior with amplitudes that depend on the values of f and r. This indicates that the SF can help to achieve and stabilize the amount of entanglement of the SLAS-SF state at a high level. The increase in the squeezed parameter r organizes and stabilizes the dynamical behavior of SSLAS and diminish the amplitude of the oscillations. On the other hand, the presence of the I-DC effect can decrease the amount of entanglement and augment the oscillations amplitude.

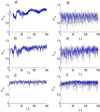thumbnail Figure 1

Temporal evolution of S A = S S LAS $ {S}_A={S}_{\mathrm{S}\mathrm{LAS}}$ for the SLAS when the field initially prepared in a SCS with | α | 2 = 25 . $ {\left|\alpha \right|}^2=25.$ The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ with different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).

3.2 Quantum coherence

The measure of coherence for a quantum state ρ is related to its off-diagonal elements by [44]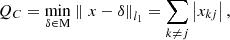 Q C = min δ ∈ M ∥ x - δ ∥ l 1 = ∑ k ≠ j | x kj | , $$ {Q}_C=\underset{\delta \in \mathrm{M}}{\mathrm{min}}\parallel x-\delta {\parallel }_{{l}_1}=\sum_{k\ne j} \left|{x}_{{kj}}\right|, $$(8)where 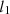l 1 $ {l}_1$ and M, respectively, describes the norm and the set of incoherent states. For different quantum states, the function QC satisfies the monotonicity property.

Now, we consider the dynamics of atomic coherence in the presence of SF. Figure 2, for a SLAS initially in an upper quantum state and the quantized field in a SCS, displays the dynamics of the measure QC with and without squeezing and I-DC effect. We can observe that the atomic coherence measure exhibits oscillations during the evolution accompanied by amplitudes that depend on f and r. The augmentation in the value of the parameter r reduces the amplitudes of the oscillations and stabilize the dynamical behaviour of the coherence measure. On the other side, the the I-DC effect can increase the amount of atomic coherence and enhance the amplitudes of the oscillations. By comparing the quantum entropy and coherence, associated with the SLAS-SF model investigated here, we find that the parameter r and the function f act on similar way on the measures of entanglement and coherence. This indicates that the coherence can be viewed as a correlation function, which can capture the correlation between subsystems.

thumbnail Figure 2

Temporal evolution of Q C $ {Q}_C$ for the SLAS when the field initially prepared in a SCS with |α|2 = 25. The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ and for different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).

3.3 Statistical properties

The Mandel QM parameter can be used to measure the deviation of the occupation number distribution from the Poissonian statistics. This parameter was introduced by L. Mandel in quantum optics [54, 55]. With negative values suggesting a sub-Poissonian statistics, it provides a practical way to describe non-classical states. It is defined as [54]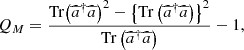 Q M = Tr ( a ̂ † a ̂ ) 2 - { Tr ( a ̂ † a ̂ ) } 2 Tr ( a ̂ † a ̂ ) - 1 ,   $$ {Q}_M=\frac{\mathrm{Tr}{\left({\widehat{a}}^{\dagger }\widehat{a}\right)}^2-{\left\{\mathrm{Tr}\left({\widehat{a}}^{\dagger }\widehat{a}\right)\right\}}^2}{\mathrm{Tr}\left({\widehat{a}}^{\dagger }\widehat{a}\right)}-1,\enspace $$(9)where 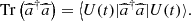Tr ( a ̂ † a ̂ ) = 〈 U ( t ) | a ̂ † a ̂ | U ( t ) 〉 . $$ \mathrm{Tr}\left({\widehat{a}}^{\dagger }\widehat{a}\right)=\left\langle U(t)|{\widehat{a}}^{\dagger }\widehat{a}|U(t)\right\rangle. $$(10)

Negative values of QM corresponds to state which a photon number variance that is less than the mean. The minimal value QM = −1 is obtained for the case of Fock states. QM > 0 corresponds to the case of super-Poissonian statistics (classical fields) and QM = 0 is for the Poissonian distribution and corresponds to case of the standard coherent state.

Let us now consider the time variation of the statistical properties of the initial SF. For this purpose, the temporal evolution of the Mandel’s parameter is plotted in Figure 3. In general, the parameter QM variation shows that the SF statistical properties exhibit a different order in terms of the squeezed parameter r. Depending on the value of r, 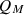Q M $ {Q}_M$ can take negative and positive values, exhibiting a sub-Poissonian and super-Poissonian distributions. On the other hand, the presence of I-DC effect does not affect the statistical features of the SF during the evolution. When r gets close to zero, the parameter 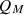Q M $ {Q}_M$ starts from a negative value and increases with the time. This indicates that the SF becomes less non-classical as the time evolves on. By less non-classical we mean here that the SF will get closer from the states that provide a Poissonian statistics.

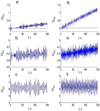thumbnail Figure 3

Temporal evolution of QM for the field initially prepared in a SCS with |α|2 = 25. The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ with different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).

4 Conclusion

In this manuscript, we have investigated the interaction between six-level atomic systems and 1-mode field initially in a squeezed coherent state. We have extended the Jeans-Cummings model to explore the interaction between the atom and the squeezed field as well as the system dynamics. We have analyzed the time evolution of the atomic coherence, non-local correlation, statistical properties within the bipartite system in the presence and absence of the intensity-dependent coupling for different squeezing regimes of the field. We have introduced the von Neumann entropy to detect the time evolution of SLAS-SF entanglement and the 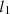l 1 $ {l}_1$ norm to investigate the dynamics of atomic coherence. We have illustrated how the amount of quantum entanglement and coherence can be affected by the nature of the SLAS-SF interaction and the initial state of the SF. By comparing the quantum entropy and coherence, associated with the SLAS-SF model investigated here, we have obtained that the squeezed parameter and the I-DC function 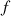f $ f$ act on similar way on the measures of entanglement and coherence. This indicates that the coherence can be viewed as a correlation function that can capture the correlation between subsystems. As a future contribution is to consider the case of open quantum system [55–57], where the system will be in contact and under the impact of its environment.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgments

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R225), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

References

  1. Jaynes E.T., Cummings F.W. (1973) Proc. IEEE 51, 89. [Google Scholar]
  2. Abdel-Aty M. (2001) Phys. A 313, 471. [Google Scholar]
  3. Abdel-Hafez A.M. (1992) Phys. Rev. A 45, 6610. [NASA ADS] [CrossRef] [Google Scholar]
  4. Berrada K., Abdel-Khalek S., Khalil E.M., Alkaoud A., Eleuch H. (2022) Chaos, Solitons & Fractals 164, 112621. [NASA ADS] [CrossRef] [Google Scholar]
  5. Gou S.-C. (1990) Phys. Rev. A 40, 5116. [Google Scholar]
  6. Li X.-S., Lin D.L., Gong C.-D. (1987) Phys. Rev. A 36, 5209. [NASA ADS] [CrossRef] [Google Scholar]
  7. Liu Z.-D., Li X.-S., Lin D.L. (1987) Phys. Rev. A 36, 1987, 5220. [NASA ADS] [CrossRef] [Google Scholar]
  8. Raffah B., Berrada K., Abdel-khalek S., Khalil E.M., Wahiddin M.R. (2020) Chaos, Solitons & Fractals 139, 109784. [NASA ADS] [CrossRef] [Google Scholar]
  9. Liu Z.D., Zhu S.-Y., Li X.-S. (1988) J. Mod. Optics 45, 833. [NASA ADS] [CrossRef] [Google Scholar]
  10. Janowicz M., Orlowski A. (2004) Rep. Math. Phys. 54, 57. [NASA ADS] [CrossRef] [Google Scholar]
  11. Wu J.-H., Li A.-J., Ding Y., Zhao Y.-C., Gao J.-Y. (2005) Phys. Rev. A 72, 023802. [NASA ADS] [CrossRef] [Google Scholar]
  12. Xue Y., Wang G., Wu J.-H., Gao J.-Y. (2007) Phys. Rev. A 75, 063832. [NASA ADS] [CrossRef] [Google Scholar]
  13. Han Y., Xiao J., Liu Y., Zhang C., Wang H., Xiao M., Peng K. (2008) Phys. Rev A 77, 023824. [NASA ADS] [CrossRef] [Google Scholar]
  14. Abdel-Wahab N.H. (2008) J. Phys. B 41, 105502. [NASA ADS] [CrossRef] [Google Scholar]
  15. Ahmed R., Azim T. (2008) J. Russian Laser Res. 29, 227. [CrossRef] [Google Scholar]
  16. Abdel-Wahab N.H., Salah A. (2017) Pramana – J. Phys. 89, 87. [CrossRef] [Google Scholar]
  17. Li Y., Hang C., Ma L., Huang G. (2006) Phys. Lett. A 354, 1. [NASA ADS] [CrossRef] [Google Scholar]
  18. Lü X.-Y., Liu J.-B., Ding C.-L., Li J.-H. (2008) Phys. Rev A 78, 032305. [CrossRef] [Google Scholar]
  19. Algarni M., Berrada K., Abdel-Khalek S., Eleuch H. (2023) Results Phys. 45, 106233. [NASA ADS] [CrossRef] [Google Scholar]
  20. Birnbaum K.M., Boca A., Miller R., Boozer A.D., Northup T.E., Kimble H.J. (2005) Nature 436, 87–90. [NASA ADS] [CrossRef] [Google Scholar]
  21. Chakram S., He K., Dixit A.V., Oriani A.E., Naik R.K., Leung N., Schuster D.I. (2022) Nat. Phys. 18, 879. [NASA ADS] [CrossRef] [Google Scholar]
  22. Eleuch H. (2009) Appl. Math. Inf. Sci. 3, 185. [Google Scholar]
  23. Sete E.A., Svidzinsky A.A., Rostovtsev Y.V., Eleuch H., Jha P.K., Suckewer S., Scully M.O. (2012) IEEE J. Sel. Top. Quantum Electron. 18, 541. [NASA ADS] [CrossRef] [Google Scholar]
  24. Zurek W.H. (2003) Decoherence, einselection, and the quantum origins of the classical, Rev. Mod. Phys. 75, 715. [NASA ADS] [CrossRef] [Google Scholar]
  25. Wen-Long Y., Yimin W., Tian-Cheng Y., Chengjie Z., Ole′s Andrzej M. (2018) Phys. Rev. B 97, 224420. [NASA ADS] [CrossRef] [Google Scholar]
  26. Streltsov A., Adesso G., Plenio M.B. (2017) Rev. Mod. Phys. 89, 041003. [NASA ADS] [CrossRef] [Google Scholar]
  27. Ollivier H., Zurek W.H. (2001) Phys. Rev. Lett. 88, 017901. [NASA ADS] [CrossRef] [Google Scholar]
  28. Bera M.N., Acín A., Kuś M., Mitchell M.W., Lewenstein M. (2017) Rep. Prog. Phys. 80, 124001. [NASA ADS] [CrossRef] [Google Scholar]
  29. Castelano L.K., Fanchini F.F., Berrada K. (2016) Phys. Rev. B 94, 23, 235433. [NASA ADS] [CrossRef] [Google Scholar]
  30. Berrada K., Eleuch H. (2019) Phys. Rev. D 100, 016020. [NASA ADS] [CrossRef] [Google Scholar]
  31. Einstein A., Podolsky B., Rosen N. (1935) Phys. Rev. 47, 777. [CrossRef] [Google Scholar]
  32. Schrödinger E. (1935) Proc. Cambridge Philos. Soc. 31, 555; 32, 446 (1936). [CrossRef] [Google Scholar]
  33. Bell J.S. (1964) Physics (Long Island City N.Y.) 1, 195. [Google Scholar]
  34. Lostaglio M., Jennings D., Rudolph T. (2015) Nat. Commun. 6, 6383. [NASA ADS] [CrossRef] [Google Scholar]
  35. Karlström O., Linke H., Karlström G., Wacker A. (2011) Phys. Rev. B 84, 113415. [CrossRef] [Google Scholar]
  36. Giovannetti V., Lloyd S., Maccone L. (2004) Science 306, 1330. [NASA ADS] [CrossRef] [Google Scholar]
  37. Berrada K. (2013) Phys. Rev. A 88, 013817. [NASA ADS] [CrossRef] [Google Scholar]
  38. Berrada K. (2017) J. Opt. Soc. Am. B 34, 1912. [NASA ADS] [CrossRef] [Google Scholar]
  39. Berrada K., Abdel-Khalek S., Ooi C.H.R. (2012) Phys. Rev. A 86, 033823. [NASA ADS] [CrossRef] [Google Scholar]
  40. Berrada K. (2014) Laser Phys. Lett. 11, 105202. [NASA ADS] [CrossRef] [Google Scholar]
  41. Plenio M.B., Huelga S.F. (2008) New J. Phys. 10, 113019. [NASA ADS] [CrossRef] [Google Scholar]
  42. Lloyd S., Phys J. (2011) Conf. Ser. 302, 012037. [NASA ADS] [CrossRef] [Google Scholar]
  43. Li C.-M., Lambert N., Chen Y.-N., Chen G.-Y., Nori F. (2012) Sci. Rep. 2, 885, 885. [NASA ADS] [CrossRef] [Google Scholar]
  44. Baumgratz T., Cramer M., Plenio M.B. (2014) Phys. Rev. Lett. 113, 140401. [NASA ADS] [CrossRef] [Google Scholar]
  45. Streltsov A., Singh U., Dhar H.S., Bera M.N., Adesso G. (2015) Phys. Rev. Lett. 115, 020403. [NASA ADS] [CrossRef] [Google Scholar]
  46. Yuan X., Zhou H., Cao Z., Ma X. (2015) Phys. Rev. A 92, 022124. [NASA ADS] [CrossRef] [Google Scholar]
  47. Winter A., Yang D. (2016) Phys. Rev. Lett. 116, 120404. [NASA ADS] [CrossRef] [Google Scholar]
  48. Greenberger D.M., Horne M.A., Zeilinger A. (1990) Am. J. Phys. 58, 1131. [NASA ADS] [CrossRef] [Google Scholar]
  49. Pan J.W., Bouwmeester D., Daniell M., Weinfurter H., Zeilinger A. (2000) Nature 403, 515. [NASA ADS] [CrossRef] [Google Scholar]
  50. Bennett C.H., Brassard G., Crépeau C.J. (1993) Phys. Rev. Lett. 70, 1895. [NASA ADS] [CrossRef] [Google Scholar]
  51. Zukowski M., Zeilinger A., Horne M.A., Ekert A.K. (1993) Phys. Rev. Lett. 71, 4287. [CrossRef] [PubMed] [Google Scholar]
  52. Stoler D. (1970) Phys. Rev. D1, 3217; 4, 1925 (1971). [NASA ADS] [Google Scholar]
  53. von Neumann J. (1955) Mathematical Foundations of Quantum Mechanics, Princeton University Press. [Google Scholar]
  54. Short R., Mandel L. (1983) Phys. Rev. Lett. 51, 384. [NASA ADS] [CrossRef] [Google Scholar]
  55. Scully M.O., Zubairy M.S. (1997) Quantum Optics, Cambridge University Press, Cambridge. [CrossRef] [Google Scholar]
  56. Eleuch H., Rotter I. (2015) Eur. Phys. J. D 69, 229. [NASA ADS] [CrossRef] [Google Scholar]
  57. Eleuch H., Rotter I. (2015) Eur. Phys. J. D 69, 230. [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Figure 1

Temporal evolution of S A = S S LAS $ {S}_A={S}_{\mathrm{S}\mathrm{LAS}}$ for the SLAS when the field initially prepared in a SCS with | α | 2 = 25 . $ {\left|\alpha \right|}^2=25.$ The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ with different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).
In the text
thumbnail Figure 2

Temporal evolution of Q C $ {Q}_C$ for the SLAS when the field initially prepared in a SCS with |α|2 = 25. The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ and for different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).
In the text
thumbnail Figure 3

Temporal evolution of QM for the field initially prepared in a SCS with |α|2 = 25. The subfigures (a, b, c) are for f ( n ̂ ) = 1 $ f\left(\widehat{n}\right)=1$ with different values of the parameter r. (a) is for r ⟶ 0, (b) is for r = 0.3 and (c) is for r = 1.5. The subfigures (d, e, f) are for the I-DC function f ( n ̂ ) = n ̂ $ f\left(\widehat{n}\right)=\sqrt{\widehat{n}}$ with the same values of r as in (a, b, c).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.